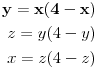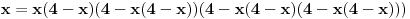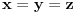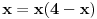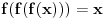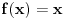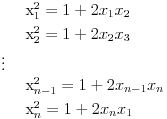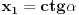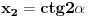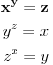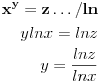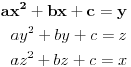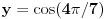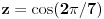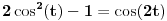[ elementarna.nepogoda @ 14.06.2012. 01:19 ] @
|
[ zzzz @ 14.06.2012. 10:13 ] @
[ Nedeljko @ 14.06.2012. 13:31 ] @
Iz cikličnosti uslova ne sledi da je
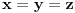 , već da ako je , već da ako je 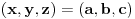 rešenje, onda su i rešenje, onda su i 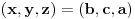 i i 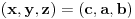 , takođe rešenja, tj. da su rešenja ciklično simetrična. , takođe rešenja, tj. da su rešenja ciklično simetrična.Zamenom se utvrđuje kom skupu mora pripadati  . To je ova jednačina osmog stepena koju je zzzz napiisao. Ona ima osam rešenja i sva su realna i jednostruka. Racionalna su 0 i 3, a faktorizacija glasi . To je ova jednačina osmog stepena koju je zzzz napiisao. Ona ima osam rešenja i sva su realna i jednostruka. Racionalna su 0 i 3, a faktorizacija glasi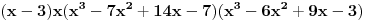 . .Iz sistema se lako vidi da su  i i  jednoznačno određeni sa jednoznačno određeni sa  , tako da svako rešenje po , tako da svako rešenje po  određuje po jednu trojku određuje po jednu trojku 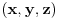 . Neposredno se proverava (a može i da se zaključi) da su svih osam dobijenih trojki rešenja. Pritom je . Neposredno se proverava (a može i da se zaključi) da su svih osam dobijenih trojki rešenja. Pritom je 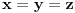 samo kod racionalnih rešenja samo kod racionalnih rešenja 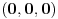 i i 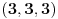 . .[ darkosos @ 14.06.2012. 13:55 ] @
[ Nedeljko @ 14.06.2012. 14:22 ] @
Za faktorizaciju polinoma sa racionalnim koeficijentima nad poljem racionalnih brojeva ima više algoritama, od kojih je jedan Kronekerov, a ja svakako nisam gubio vreme na to, već se poslužio programom wxMaxima.
[ elementarna.nepogoda @ 14.06.2012. 14:58 ] @
Hvala na odgovorima.
Ostaje samo pitanje kako u realnim uslovima, tj na ispitu koji traje 4 sata, efektivno doci do navedene faktorizacije ? btw. Blanket sadrzi 8 zadataka i svaki se radi na neku foru koje se treba dosetiti za dato vreme. [ Nedeljko @ 14.06.2012. 17:58 ] @
Nađeš racionalne nule, pa podeliš polinom sa
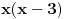 . Ostaće ti polinom . Ostaće ti polinom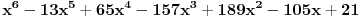 Najpre, po Gausovoj lemi je polinom sa celobrojnim koeficijentima rastavljiva nad poljem racionalnih brojeva akko je rastavljiv nad prstenom celih brojeva. Dakle, tražimo celobrojna rastavljanja. Prvo se konstatuje da nema linearnih činioca jer nema rcaionalnih korena. Pretpostavimo da ima činilaca stepena dva sa celim koeficijentima, tj. da se može napisati kao proizvod polinoma stepena dva i četiri sa celim koeficijentima. Bez umanjenja opštosti možemo pretpostaviti da je vodeći koeficijent činioca stepena dva pozitivan. Samim tim, takav mora biti i vodeći koeficijent činioca stepena četiri. No, pošto je njihov proizvod jednak 1, onda svaki od njih mora biti 1. 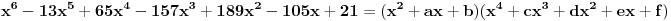 . .Prvo, 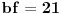 , pa , pa 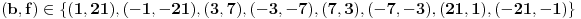 . .Ako je npr. 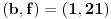 , onda jednakost , onda jednakost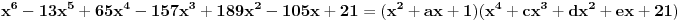 postaje sistem 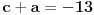 , ,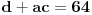 , ,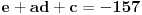 , ,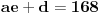 , ,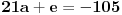 . .Dakle, imaš pet jednačina sa četiri nepoznate, pa petljaj s njima malo dok ne dobiješ kontradikciju. Recimo iz prve jednačine možeš da eliminišeš c, a iz pete e. 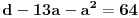 , ,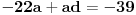 , ,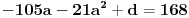 . .Oduzimanjem prve jednačine od treće dobija se da je 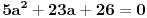 , ,čije je celobrojno rešenje -2. Zamenom dobijamo da je 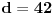 , ,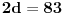 , ,što je očigledna kontradikcija. Tako se odbaci jedan po jean od parova kandidata za 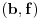 i konstatuje da nema činilaca sa celim koeficijentima stepena 2. Na sličan način se radi i sa činiocima stepena 3, s tim da, pošto su istog stepena, možemo pretpostaviti da je apsolutna vrednost slobodnog člana prvog činioca veća ili jednaka apsolutnoj vrednosti drugog činioca, pa imamo četiri slučaja umesto osam. Naravno, čim pogodimo jedan činilac, završili smo posao. Nema potrebe razmatrati i ostale slučajeve. i konstatuje da nema činilaca sa celim koeficijentima stepena 2. Na sličan način se radi i sa činiocima stepena 3, s tim da, pošto su istog stepena, možemo pretpostaviti da je apsolutna vrednost slobodnog člana prvog činioca veća ili jednaka apsolutnoj vrednosti drugog činioca, pa imamo četiri slučaja umesto osam. Naravno, čim pogodimo jedan činilac, završili smo posao. Nema potrebe razmatrati i ostale slučajeve.Lično ne smatram da je ovakav zadatak primereno dati kao jedan od četiri zadatka na ispitu koji traje četiri sata. No, to je na onima koji zadaju zadatke da odmere vreme potrebno za njihovu izradu. [ elementarna.nepogoda @ 14.06.2012. 19:21 ] @
Hvala puno.
Citat: Nedeljko: Lično ne smatram da je ovakav zadatak primereno dati kao jedan od četiri zadatka na ispitu koji traje četiri sata. No, to je na onima koji zadaju zadatke da odmere vreme potrebno za njihovu izradu. Ispravka, jedan od 8 zadataka. Da ne spominjem da se na konsultacijama ovaj i jos neki zadaci rade satima, a dobijaju odgovori oblika " Ja ovde ne vidim resenje.. " . Dalje, bilo je i zadataka tipa dokazati nejednakost, ali je znak obrnut (pronadjen kontraprimer na ispitu.... ) . No, to je neka d(r)uga prica. Hvala jos jednom na pomoci. [ Nedeljko @ 14.06.2012. 21:58 ] @
Ako je tako, onda će biti da su postavljači mislili na ono što je zzzz napisao, tj. da nemaju pojma i tako svojim neznanjem zeznu one koji znaju i otele se da urade do kraja.
[ elementarna.nepogoda @ 25.06.2012. 21:01 ] @
[ Nedeljko @ 26.06.2012. 10:02 ] @
Pa, sjajno si počeo. Pošto se u slučaju da je
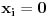 jednačina jednačina 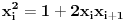 svodi na svodi na 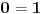 nijedna promenljiva ne sme biti jednaka nuli, pa je sistem ekvivalentan sa nijedna promenljiva ne sme biti jednaka nuli, pa je sistem ekvivalentan sa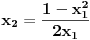 , ,... 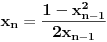 , ,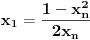 . .Neka je sada 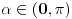 takvo da je takvo da je 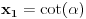 . Indukcijom se lako proverava da je . Indukcijom se lako proverava da je 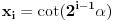 . Uslovu . Uslovu 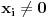 odgovara uslov odgovara uslov 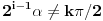 , odnosno , odnosno 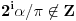 . .E, sad, na osnovu poslednje jednačine je 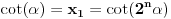 , pa je , pa je 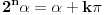 , odnosno , odnosno 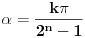 . Uslov . Uslov 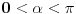 daje daje 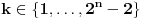 . .[ elementarna.nepogoda @ 26.06.2012. 12:22 ] @
Hvala puno na pomoći.
Da, znam da je 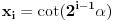 ali ne znam da li i to treba dokazivati, budući da argumenti kotangensa čine geometrijski niz uslovno rečeno. ali ne znam da li i to treba dokazivati, budući da argumenti kotangensa čine geometrijski niz uslovno rečeno.Korak koji mi je nedostajao bio je 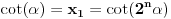 Još samo jedan detalj: Često je deo zadatka i pitanje koliko sistem ima rešenja. Da li odgovor dobijam prebrojavanjem skupa 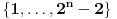 iz koga je k? Odnosno iz koga je k? Odnosno 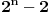 . I zašto uopšte . I zašto uopšte 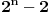 ? Da nije ? Da nije 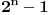 ? ?[ Nedeljko @ 26.06.2012. 13:54 ] @
Da, svako k će ti dati po jedan sistem rešenja. Granica za k proističe iz granice za alfa. Pogledaj malo bolje.
[ zzzz @ 26.06.2012. 19:33 ] @
Zar nije (?:
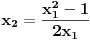 i slijedi smjena: i slijedi smjena: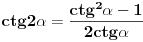 itd.. itd..Ali i ovdje uočavam ovakvo trivijalno rješenje: 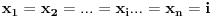 ..... .....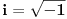 Sad mi se nešto čini da bi i prvi zadatak trebao ići na ovakav štos, naprimjer ako transforišemo 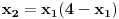 u.. u..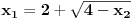 Ne vidim koja je funkcija zgodna za smjenu.Ili da nije greška u zadatku? Ona faktorizacija mi izgleda preobiman posao,gotovo nemoguć. [ elementarna.nepogoda @ 27.06.2012. 12:46 ] @
[ elementarna.nepogoda @ 28.06.2012. 19:47 ] @
[ darkosos @ 28.06.2012. 21:34 ] @
Nesto sam krenuo ovako, vidi dal' je ok:
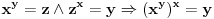 pa kad dodamo jos pa kad dodamo jos 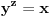 dobija se dobija se 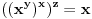 iliti iliti 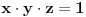 . .E sad, ja sam nesto gledao, ako pretpostavimo da je x > 1, onda je, zbog uslova da su x, y i z pozitivni, 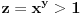 i zato i i zato i 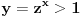 . Naravno, posto je proizvod 1, ne mogu sva tri biti veci od 1. Analogno bi trebalo da se dobije i za . Naravno, posto je proizvod 1, ne mogu sva tri biti veci od 1. Analogno bi trebalo da se dobije i za 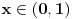 , samo sada ispadaju svi manji od 1, pa opet ne moze... , samo sada ispadaju svi manji od 1, pa opet ne moze...[ Nedeljko @ 28.06.2012. 21:42 ] @
Bravo, darkosos! x=y=z=1 je jedino rešenje.
[ elementarna.nepogoda @ 28.06.2012. 21:51 ] @
bravo Darko.
Hvala puno. [ Nedeljko @ 16.12.2012. 02:25 ] @
[ nePonovljivA @ 16.12.2012. 08:09 ] @
Hm...
Zapravo, zadatak je bio dokazati da dati sistem nema realnih rešenja ako cu a,b,c brojevi takvi da je  . . Ako je x=y=z, tada se ova pretpostavka lako primenjuje, jer imamo kvadratnu jednačinu čija je diskriminanta po pretpostavci negativna. Ostaje da se pokaže da je zaista x=y=z jediina mogućnost. Ako imaš bolju ideju.... [ Nedeljko @ 16.12.2012. 11:46 ] @
Kako misliš da li imam ideju da dokažem nešto što nije tačno? Trebala si da postaviš zadatak onako kako glasi. Ovakva postavka jednostavno nije tačna.
Ako je 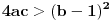 , onda je svakako , onda je svakako 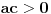 , pa samim tim i , pa samim tim i 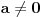 . Stoga svaku od jednačina možemo pomnožiti sa . Stoga svaku od jednačina možemo pomnožiti sa  i dodati obema stranama i dodati obema stranama  . Uz smenu . Uz smenu  , , 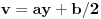 i i 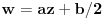 i uz oznaku i uz oznaku  sistem postaje sistem postaje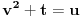 , , , , . .Obzirom da je 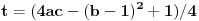 , važi , važi  . Naime, odatle sledi da je . Naime, odatle sledi da je 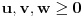 , a pošto je , a pošto je 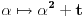 rastuća funkcija na rastuća funkcija na 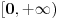 iz iz  sledi sledi  , a odatle , a odatle 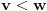 , a , a  neće da može. Takođe, iz neće da može. Takođe, iz 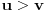 sledi sledi 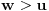 , a odatle , a odatle  , a , a 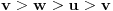 opet neće da može. Ostaje da je opet neće da može. Ostaje da je  , a otuda i , a otuda i  . Međutim, onda je . Međutim, onda je 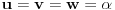 za za  za koje je za koje je 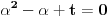 , odnosno , odnosno  , što nije moguće za , što nije moguće za  jer je leva strana nenegativna, a desna negativna. jer je leva strana nenegativna, a desna negativna.Dakle, uz uslov 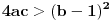 je lako. Međutim, taj uslov nisi pominjala. Ovo je sasvim drugi zadatak. je lako. Međutim, taj uslov nisi pominjala. Ovo je sasvim drugi zadatak.Edit: Ispravka greške. [Ovu poruku je menjao Nedeljko dana 16.12.2012. u 16:21 GMT+1] [ nePonovljivA @ 09.05.2013. 17:41 ] @
y+1=(x+1)(3-x)
z+1=(y+1)(3-y) x+1=(z+1)(3-z) Treba rešiti dati sistem u skupu R. Ja primećujem da je y=f(x), z=f(y), x=f(z), (što ne umem dalje da iskoristim) gde je f kvadratna f-ja. Dalje, primećujem da su rešenja (2,2,2) i (-1,-1,-1). Ne znam kako ide formalno rešenje, pa mi treba pomoć. Isto bi mi dobro došla i literatura sa ovim cikličnim sistemima jer ih profesor stalno daje, a neće da kaže odakle da uvežbamo. Obično rešenje ide u smeru dokazivanja da je x=y=z. Meni bi značili neki primeri iz kojih mogu da pohvatam bar neke ideje kako se to pokazuje. [ Nedeljko @ 09.05.2013. 20:05 ] @
Za
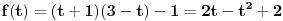 je je 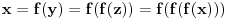 . Dakle, . Dakle, 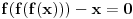 . Faktorizacijom ove jednačine dobijamo da je . Faktorizacijom ove jednačine dobijamo da je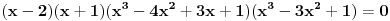 . .Dakle,  može biti može biti  ili ili  ili koren jednog od navedena dva kubna polinoma. Ako je ili koren jednog od navedena dva kubna polinoma. Ako je 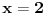 ili ili 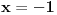 , onda je svakako , onda je svakako 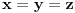 . .Sa druge strane, ako je 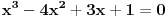 , onda su i , onda su i  i i  koreni istog tog polinoma i to međusobno različiti, jer kada bi na primer bilo koreni istog tog polinoma i to međusobno različiti, jer kada bi na primer bilo  , onda bi zbog , onda bi zbog 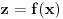 ta vrednost bila nepokretna tačka funkcije ta vrednost bila nepokretna tačka funkcije  , a to su samo , a to su samo  i i  , što nisu koreni tog polinoma trećeg stepena. , što nisu koreni tog polinoma trećeg stepena.Isto važi i u slučaju 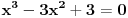 važi analogno. važi analogno.Dakle, ili je 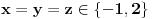 ili su ili su 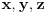 koreni istog od navedena dva kubna polinoma, ne u bilo kojoj permutaciji, nego u tri od šest mogućih permutacija, odnosno, ne mora biti koreni istog od navedena dva kubna polinoma, ne u bilo kojoj permutaciji, nego u tri od šest mogućih permutacija, odnosno, ne mora biti 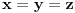 . .[ nePonovljivA @ 09.05.2013. 20:23 ] @
Hvala.
A jel možeš malo da pojasniš kako doći do pomenute faktorizacije? [ Nedeljko @ 10.05.2013. 17:31 ] @
Obzirom da se u polinomu kao koreni moraju pojaviti sve vrednosti koje mogu učestvovati u rešenju, on mora biti deljiv sa [tex[(x+1)(x-2)[/tex], pa ga deli s tim koliko god je moguće, a moguće je jednom (jer -1 i 2 su jednostruke nule tog polinoma).
Ostaće ti polinom šestog stepena. Pomnoži ga sa -1 sa bi bio moničan. Možeš da pokušaš da ga faktorizuješ kao proizvod polinoma drugog i četvrtog stepena, pa kada se pokaže da ta faktorizacija ne postoji, onda kao proizvod dva kubna polinoma. Obzirom da je polinom moničan, možeš se ograničiti na slučaj da su činioci monični. Obzirom da je slobodni član jednak 1, imaš dva slučaja - da su slobodni članovi činioca jednaki 1 i da su jednaki -1. E, onda sve rešavaš metodom neodređenih koeficijenata. Staviš da su ostali koeficijenti činioca neodređeni, pa pomnožiš činioce, pa proizvod izjednačiš sa datim polinomom. Dobićeš sistem jednačina po neodređenim koeficijentima. On će odmah moći da se uprosti korišćenjem dve linearne jednačine kojima se red sistema snižava sa dva. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|