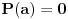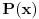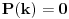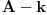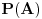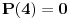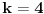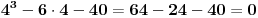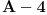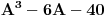[ duksi1993 @ 14.06.2012. 19:31 ] @
|
| Poštovani,
naišao sam na zadatak, u kojem se na određenom koraku dolazi do jednačine tipa:
x3 + px + c = 0
tačnije, primer (A3 - 6A - 40 = 0), koja kada se razloži izgleda ovako: (A-4)(A2 + 4A + 10) = 0.
E sad, mene zanima, način na koji je razložena gornja jednačina.
Napomena: Razloženu jednačinu sam našao u gotovom rešenju zadatka (u knjizi), ali nisam uspeo da samostalno dođem do nje.
Da li postoji neko pravilo vezano za to?
Unapred hvala. |
[ darence @ 14.06.2012. 20:41 ] @
Recimo preko Bezuovog stava.
[ duksi1993 @ 14.06.2012. 20:47 ] @
Bezuov stav važi samo za jednačinu oblika:
x3 + ax2 + bx + c = 0.
Probao sam da ga primenim u ovom slučaju, ali bezuspešno.
Ova jednačina nema ax2
[ Sonec @ 14.06.2012. 20:58 ] @
Bezuov stav kaze ako je
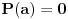
tada

deli
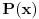
. Nema on nikakva ogranicenja sto se tice samoga oblika polinoma.
[ Sini82 @ 14.06.2012. 21:10 ] @
[ duksi1993 @ 14.06.2012. 21:42 ] @
Samo jos jedna stvar...
Ako x-a deli polinom P(a), kako je u ovom slučaju a = 4?
Samo mi to nije jasno...
@Sini82, pogledao sam link...
Tim pravilom se vraćam na početak zadatka...
Meni je to dato, pa ja stižem do gore napisane jednačine... :)
[ darkosos @ 14.06.2012. 21:49 ] @
O ovome je bilo puno puta na forumu, pretrazi malo... Imas i ovde
http://en.wikipedia.org/wiki/Rational_root_theorem
[ Sonec @ 14.06.2012. 21:58 ] @
Citat:
duksi1993: Samo jos jedna stvar...
Ako
x-a deli polinom
P(a), kako je u ovom slučaju
a = 4?
Samo mi to nije jasno...
Obrati paznju sta sam ja napisao
Citat:
Sonec: Bezuov stav kaze ako je
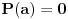
tada

deli
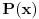
.
Dakle, u mom slucaju je polinom po

.
U tvom slucaju je polinom po

i ako nadjes broj

takav da je
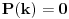
onda
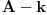
deli
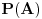
. Kod tebe je
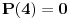
(
) jer je
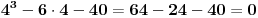
, pa
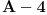
deli polinom
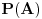
.
[ Sini82 @ 14.06.2012. 22:06 ] @
Na linku koji sam ti postavio imaš opisan postupak kako se rješava kubna jednačina tipa koji tebe zanima. Kada nađeš nule, lako je izvršiti faktorizaciju (jedina realna nula je 4 pa je polinom
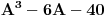
djeljiv sa
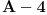
, druge dvije su kompleksne; dijeljenjem ova dva polinoma dobijaš drugi član u faktorizaciji; možeš ovdje da provjeriš
http://www.easycalculation.com/algebra/cubic-equation.php ).
[ elementarna.nepogoda @ 14.06.2012. 22:34 ] @
covek se logicno pita kako da pogodi bas broj a za koji je p(a)=0. Taj broj trazi se medju deliocima slobodnog clana, u ovom slučaju broja 40.
[ Sini82 @ 14.06.2012. 22:49 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.