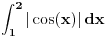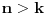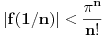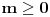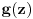Naravno, zadaci bi morali da budu odgovarajući, a ne prosta primena formula za koje studenti posle ne znaju šta će im. E, ali onda i nastava treba da bude takva da obučava studente za rešavanje matematičkih i nematematičkih problema matematičkim metodama.

Da, to jeste taj problem sto bi se onda neki zadaci mogli resiti bez previse znanja o materiji. Mozda je bolja ideja uradii obrnuto, dati kontrolisan skup informacija na koriscenje. Malo bi bilo nezgodno za matematicki program, kako iskljuciti opcije? Ali, npr. kao u skorasnjoj temi sa "ciklicnim" sistemom, ako imas program, uradis rastavljanje (i odredjivanje nula) pre nego kazes keks. Sa druge strane, zadaci koji traze ideju su npr. 1 ili najvise 2 zadatka na ispitu, makar je tako bilo u moje vreme. Ostalo je prakticno rutina. Dakle spemanje zadataka bi postalo jos nezgodnije, pa bi tako nesto prakticno znacilo revoluciju u obrazovanju (kao sto je to bio digitron :)).

Zamisljam sada ovako nesto: umesto klasicnog matematickog programa, dati nesto kao "jelovnik za racun", gde bi se kontrolisalo sta se pita. Npr. pokrenes program, izaberes od ponudjenih opcija sta zelis da izracunas i posaljes pitanje, dobijes odgovor. Nesto kao matematicki firewall :) A onda onaj ko daje zadatke mora da podesi i firewall. Posto postoje ti command line programi, ovo bi moglo relativno jednostavno da se odradi. Uz ovo bi naravno trebalo da postoji i jelovnik formula.

Poenta je čemu na ispitu zadaci koje računar rešava automatski? Kakva je praktična kmorist od tog znanja? Kakva je korist od znanja dokaza sto kila teorema, pri čemu svaki od tih dokaza piše u svakoj knjizi? Da li je sa pojavom matematičkog softvera prestala potreba za matematikom? Naravno da ne. Praktičan problem je što gro predavača nemaju pojma o značaju onoga što predaju i što ne umeju da prave takve zadatke. Pojavom matematičkog softvera nije prestala potreba za matematikom, nego za takvim matematičarima.

Svojevremeno su na pismenom iz osnova geometrije u Beogradu sva četiri zadatka bila za razmišljanje. Onaj zadatak o ciličnom sistemu jednačina je zahtevao razmišljanje, jer da nije, postavljač teme bi ga samostalno rešio i ništa ne bi pitao. Takođe se zzzz kao pristojan matematičar na ovom forumu okliznuo. Lako je meni bilo da faktorišem polinom korišćenje programa wxMaxima, ali je trebalo doći do tog polinoma i znati šta posle s njim raditi. U tome je stvar, a ne da računam broj pi na sto decimala na ruke.

Pa danas racunar zna svasta da resi automatski, nisam siguran da sve to student sme da ne zna... Uostalom, ko ce da pravi dalje te programe pa i samo da odrzava :) Mozes da kazes da npr. posto se rastavljanje na cinioce ozbiljnije radi u srednjoj skoli, da tada ucenik ne sme da koristi pomocna sredstva. A da kasnije, kada mu to zatreba, moze da uradi masina, jer on vec zna kako se radi, a sto da trosi vreme, kad to ionako nije poenta...

Ali ja bih svakako uveo pravilo da u toku skolovanja svaka racunska metoda mora da prodje "kroz ruke" (mozda sa izuzetkom nekih smorova tipa n-ti koren, logaritmi ili slicno - ali svakako metode koje se rade simbolicki). Pa kako postoje metode koje se uce tek na studijama, onda bi to moralo da vazi i za takve metode. E sad, kako ce neko da odvoji sta se podrazumeva da student zna (tj. da je presao to na ruke), a sta je tematika samog kursa? Pa tako sto ce, kao sto sam predlozio, da se napravi spisak sta student moze da uradi pomocu masine a sta ne.

Na kraju krajeva, i samo znanje pesackog tipa mora da se obnavlja. Kao sto si i sam rekao na nekoj temi ovde skoro, mozda bi neko ko pise knjige mogao da napise iz glave, ali nekako je to moralo u tu glavu da stigne. Pa na primer i sam predavac, zar bi mogao da prikaze dokaz necega a da ne prodje kroz detalje, gde ponekad oni takodje zahtevaju dosta osnovnog racuna. Da li prihvatio dokaz koji je uradila masina? Postoji i takav softver. A onda, ako to zahtevamo od predavaca, zasto da ne zahtevamo od studenata. Potpuno se slazem da ne sme "ranije predjeno gradivo" da prevazidje tematiku kursa, ali ovo je nesto drugo. Kao sto si svojevremeno ucio sabiranje kroz puno primera, sredjivanje algebarskih izraza, ucio tablicu mnozenja napamet, tako moras da prodjes i kroz tablicne integrale, standardne tehnike resavanja i puno zadataka "na ruke". Zato da bi kasnije znao i da uradis neki komplikovaniji zadatak - naravno to je samo potreban uslov :)

Taj softver će da piše onaj ko prouči te metode, a to je onaj ko je naučio da misli. Pretpostavljam da si programer u nekom višem programskom jeziku. Ima li leba bez asemblera? Pa, ima. Naravno da prevodioce mora neko da napiše, ali to je radio neko ko sjajno zna asembler. Ne moraju i ne mogu svi znati sve. Stekni nekakva upotrebljiva znanja i koristi ih. To mogu da budu i asembler i teorija prevođenja. OK, i to treba neko da zna.

Sa druge strane, što se prolaska osnovnih metoda na ruke tiče, to može da se pita na usmenom, a na pismenom da se proverava operativno znanje. Na kraju, Bojan Bašić je pominjao neku teoremčinu koja se dokazuje na trocifrenom broju strana i za koju na studijama nema vremena da se izvodi njen dokaz. Da li je to razlog da se ta teorema ne uči i ne primenjuje? Pa, ne. Jednostavno treba reći gde se dokaz može naći, pa ko hoće, neka ga nauči, a na vežbama da se rade primene te teoreme.

Pretpostavljam da si mene pomenuo zbog toga što znaš da dozvoljavam korišćenje bilo kakve literature (u papirnom obliku) na kolokvijumu/pismenom ispitu, pa pitaš smatram li da je ovo logičan sledeći korak. Ako bi se ovo što predlažeš moglo u praksi izvesti, apsolutno bih bio za to. No, tako nešto ipak je praktično nemoguće. Prvo, ako bi se omogućio izlaz na internet (za šta takođe smatram da bi bilo u redu — uz, jasno, zabranu komunikacije s drugim licima), bilo bi nemoguće kontrolisati upravo komunikaciju s drugim licima. Drugo, i ako je izlaz na internet onemogućen, opet će se u praksi teško dogoditi da fakultet omogući laptopove svim studentima na svim ispitima. (Što se tiče predmeta koji se polažu na kompjuterima, u računarskim učionicima, to obično biva dosta nezgodno — ispiti traju po više dana, mora se praviti zilion grupa zadataka, i sve to funkcioniše samo zahvaljujući tome što takvih ispita ima dovoljno malo; ako bi se svi ispiti održavali u računarskim učionicama, otišlo bi sve u majčinu.) Varijanta da svaki student donese svoj laptop takođe je neprihvatljiva, počev od toga što se time u startu favorizuju studenti koji imaju laptopove (a nemaju ih svi, niti imaju svi novca da ih kupe), pa nadalje. I najzad, u bilo kom od poslednja dva scenarija, studenti bi mogli prokrijumčariti mobilni internet u amfiteatar (cenim da modem u formi USB stika ne bi bilo previše teško uneti u amfiteatar i krišom ga uštekati u USB port), a time opet puca cela koncepcija.

Dakle, zaključak: teorijski, veoma se slažem s idejom koju si izneo; praktično, ona je neostvariva.


Nažalost, apsolutno si u pravu.

Iako poredjenje sa programiranjem ina smisla, ipak prakticno programiranje nije nauka. Mnogo puta napisem nesto i ne razmisljam previse da li je to 100% ok, vec pustim prvo da masina iskompajlira, dakle da prodje sintaksno, pa onda pokrenem da vdim da li radi kako treba, a nerertko se desava i da se mnogo kasnije nadje neki "bug". Ja sam sklon da kazem da je programiranje slicnije zanatu. Pa tako koristim alatke koje su drugi napravili, kao sto nas svih nema, u savremenom drustvu, bez mnogo stvari o kojima ne razmisljamo, npr. da neko negde treba da pozanje, zavari, stisne... To su preduslovi da mi "odemo dalje" i da koristimo stvari kao sto su racunar, internet...

Ali ovde je to sve deo jedne celine, i cak bih rekao da potpomaze napredovanju. Uostalom, nije mi jasno sasvim koja ti je ciljna grupa? Talentovani studenti matematike? Ili svi koji imaju matematiku kao predmet na studijama?

Bojane,

Nisam tebe prozvao samo zbog toga što si naveo, već i zato što se zalažeš za učenje i onih teorema koje se ne mogu dokazivati na predavanjima i njihovu primenu i zbog toga što smo se složili oko toga gde je mesto analitičkom i sintetičkom pristupu u geometriji (rasprava u čuvenom "metodu pogrešne discipline").

Ako se teorijski slažeš, onda bih u vezi praktičnog sprovođenja rekao sledeće: Sve mašine bi morale da budu fakultetske i nijedan student ne bi imao pravo da donese svoju mašinu. To dalje otvara mogućnost da fakultetsko računarsko osoblje izvadi iz hardvera sve komponente koje se mogu koristiti za pristup internetu. Dakle, nema antene za bežični internet, niti USB priključka. Ima DVD čitač, koji bi fakultet koristio za instalaciju softvera, pa student neka na diskovima donese šta god hoće. Štaviše, može se koristiti izmenjeno linuks jezgro bez podrške za umrežavanje.

Problem je cena svih tih laptopova. Ali, hej, koliko ono fakultet uzima keša po studentu, što od studenata, što iz budžeta? Zar je 70 evra za polovnu mašinu, koja bi trajala dve do tri godine veliki izdatak? Takođe, neka svaki student plaća 100 dinara po ispitu za struju koju će da potroši.

E, sad, glavni i ključni problem je nastavni kadar, koji ne zna da smisli drugačije zadatke od

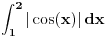
koji u XXI veku ne služe skoro ničemu.


darkosos,

Programiranje je zanat pravljenja programa, a matematika zanat pravljenja teorema i njihova primena. U oba slučaja se koriste prethodni rezultati i prave i ispravljaju bagovi. Naravno da čovečanstvo treba da sačuva sva bitna znanja, ali ja koristim deterdžente nemajući pojma o hemiji, jer to zna neko drugi, a ja znam nešto drugo, što ću da unovčim da bih kupio deterdžent.

Posto je poenta pitanja da li se moze na ispitima dozvoliti sva literatura (veliki deo literature je vec digitalizovan) i usput omoguciti dosta simbolickog racuna ja nisam siguran da je ovo prakticno dobra ideja, iako bi teoretski dala dosta dobre rezultate.
Naravno, da bi odgovori bili precizniji trebalo bi imati informaciju da li se radio o osnovnim studijama, masteru ili nesto vise od toga, ali polazim od pretpostavke da se radi o osnovnim studijama.
Kljucni momenat za nastavak diskusije smatram u kriterijumu koji ispitivac postavi za osnovu ispita tj. kako postavlja pismeni zadatak tj. koju tezinu zadataka daje.

Ako je poenta dozvoliti "sve" (osim komunikacije sa drugima na sipitu) a dati takve zadatke da ti ta "sva" literatura moze malo ili nimalo pomoci na ispitu onda nisam siguran da je to OK pristup, cak sta vise to cesto bude "ometajuci faktor" jer se daje lazna sigurnost studentima da ce nesto korisno isceprkati.
Mislim da je osnovni pristup da se definisu znanja koja student treba da usvoji za dati predmet, da se zatim te teme kvalitetno obrade na predavanjima i vezbama i da zatim ispit bude provera usvajanja tih znanja, i prilagodjen vremenu od npr. 4h.
Kvalitet na ispitu treba biti podrzan kvalitetom pre ispita.
Jer u cemu je poenta dati nesto na ispitu sto nije obradjivano na vezbama i predavanjima? Ili biti tako formulisano da student treba uloziti ogroman napor da bi prepoznao i povezao zadatak sa ispita sa obradjenom teorijom i zadacima na predavanjima i vezbom (govorim o npr. zadacima za 6 ili 7).

I tu dolazim do poente zasto ja ne bih dozvoljavao bas sve na ispitu.
Formule, potrebne teoreme i slicne stvari da, ali ne i ostalo.
Naravno, ne podrazumeva sve ovo da svi zadaci budu takve tezine da ako predjete vezbe ladno mozete dobiti 10, ali da to bude dovoljno za barem 6 ili 7.
Za vece ocene, naravno, trebalo bi formirati ostriji kriterijum.

I skoro da mi nikad nije bilo jasno sta profesori (ispitivaci) tacno ocekuju od studenta na ispitima tj. sta to znaci dobiti 10?
Da li je to kompletno savladan program za taj ispit, za odgovarajucim znanjem u pismenom i usmenom delu ili to znaci nesto sire od toga?
Da li to znaci da kada neko uradi 5 zadataka (100%) na ispitu to znaci da on zna sve ili je jednostavno imao inspiraciju, dobar dan ili zadatke koji su mu isli na ruku?
A moje misljenje je da bi trebalo i pismeni ispit imati vise nivoa za studente koji pokazuju dobra znanja i idu na visoku ocenu jer smatram da se sa 5 zadataka ne moze stvoriti bas neka realna slika o znanjima studenta.

Princip neke standardizacije znanja mislim da je vrlo ozbiljno pitanje i deluje mi da se dosta olako prelazi preko njega i da postoji jako velika sarolikost po ovom pitanju i dosta toga je ostavljeno na savesti profesoru, sto je cesto povod za razne zloupotrebe.
Neki imaju ambicije da sto vise nauce studente a neki da od ispita naprave "baba rogu".

Nedeljko, imam utisak da nece biti lako poloziti ispit kod tebe, pa taman im dozvolio i internet

Imali smo jedan takav predmet-vežbe-ispit. Sve se svelo na to da smo koristili gotove programe, koje je asistentkinja pravila namenski za to specifično gradivo (numerička analiza), da smo katkad samo ubacivali podatke u sličan već urađen zadatak na vežbama (dakle, nije nam na raspolaganju bila samo Wolfram Mathematica), vreme za izradu zadataka je bilo knap, kolokvijuma nekoliko... Uđeš, zarumeniš se brzo razmišljajući i radeći, izađeš, zaboraviš i - gotovo.

Kao što bi pri izradi nekih zadataka bilo mnogo udobnije da se mašina bavi determinantama ili sistemima jednačina, moguće je i napraviti dogovor da se na ispitu iz npr. diferencijalnih jednačina pri rešavanju sistema Lagranžovom metodom ne izračunava sve do kraja, jer nije poenta u izračunavanju silnih integrala. U pomenutoj numeričkoj analizi zgodno je iscrtati grafik funkcije i napraviti solidnu ocenu njenog ekstrema, ali ne vidim baš mnogo drugih predmeta gde bi prednost za ispitivača i studente bilo korišćenje računara. Doduše, ja sam "stara garda" i preferiram više one ispite na kojima se dobiju lepi zadaci za razmišljanje, pa kad na kraju dođeš do ideje, osećaj zadovoljstva te još dugo drži.

Moje poredjenje sa zanatom je imalo drugaciji smisao - da zanatlija radi svoj posao ne razmisljajuci mnogo zasto i kako nesto radi (naravno da moze i da zna, ali nije neophodno). On zna da ako uradi to ovako - da ce ispasti onako. A vremenom dolazi do iskustva za razne situacije. Ali nema potrebu da napravi teoremu o tome. Taj korak da napravi od poznatog nepoznato se moze zvati izum, ali nije neophodni deo zanatstva. Po meni, zanatski deo matematike je bas taj koji hoces da izbacis.

Lepo je videti kako se javlja sve više učesnika na ovoj temi sa kreativnim i konstruktivnim komentarima.


igorpet

Nije uopšte poenta da se studntima zagorča život na ispitu. "Kuku majko, koliko ih je položilo." Ne. Poenta je da što veći broj ljudi stekne što upotrebljivije znanje. Ako je lako položiti ispit, onda postoji problem, ali ne u tome što je masa položila, već u tome što se sa razumnom težinom moglo naučiti više. Dakle, otežaj ispit proširivanjem sadržaja, a ne teranjem studenata da drndaju determinante i faktorizaciju polinoma u ekstremno kratkom vremenskom roku.


darkosos

Zanatljija mora da napravi bravu koja radi. Ako on ne zna šta treba da zna u vezi pravljenja pumpi, neće moći ni da je napravi. Isto je i sa pravljenjem teorema. Kao što obućar ne mora da razume međumolekularne sile da bi nešto zalepio, već samo da zna kako to da uradi, tako i matematičar istraživač treba da zna samo koja mu teorema treba i kako tačno glasi, a ne i njen dokaz.

Svojevremeno nam je asistent iz verovatnoće i statistike zadao zadatak koji je ekvivalentan velikoj Fermaovoj teoremi. OK, neko je dokazao tu teoremu i dokaz je proverio veliki broj stručnjaka iz oblasti. Dakle, tvrđenje je tačno. Treba li zbog toga što ne znam dokaz velike Fermaove teoreme da je ne primenjujem?

darkosos

Evo ti jednog konkretnog primera. RSA algoritam je zasnovan na težini faktorizacije prirodnih brojeva. Najjednostavniji algoritmi faktorizacije su eksponencijalne složenosti u odnosu na broj cifara ulaza, ali postoje napredni koji su subeksponencijalne složenosti (ali ne i polinomijalne). No, oni su jako složeni. Da bi studenti računarstva mogli da izračunaju koliki si potrebni računarski resursi za razbijanje RSA sa nekim brojem bitova širine, oni moraju znati složenost problema faktorizacije prirodnih brojeva. Da li to znači da to od njih treba kriti kao zmija noge, jer zaboga, materija je kompleksna da bi se izložila sa dokazima iako je potrebna formulacija dovoljna za račun sasvim jednostavna?

Zapravo, ovde se mora poći od toga šta je cilj nastave, pa onda prema svecu i tropar. Ja sam tako razmišljao.

Trudimo se da budemo konkstruktivni, a ono sto se meni licno svidja u zadnje vreme na forumu je nivo diskusija, koje su po meni, dostigli jedan pristojan akademski nivo.

A sto se tice "dizanja kriterijuma", pa sad to zavisi od predvidjenog plana i programa rada i ja nisam da se to radi u zavisnosti od prolaznosti.
U stvari najbolje bi bilo kad bi realno steceno znanje omogucavalo da student polozi ispit u nekom razumnom roku (2-3 ispitna roka) i to bi, prema meni, znacilo visok nivo kvaliteta vezbi i predavanja i motivisanosti studenata a ne nesto trece.
A "dizanje nivoa" trebalo bi da se odnosi i na kvalitet nastave i da to bude u srazmeri i tada bi po meni bilo OK.

A ako poenta zadatka nije npr. determinanta ili prost racun, faktorizacija ili nesto slicno dovoljno je omoguciti studentima one malo naprednije digitrone ili eventrualno u dozvoljenim formulama navesti primere resenja 10-ak determinanti ili neke faktorizacije koje mogu biti deo nekog zadatka i time dati gotova resenja tog dela zadatka. Da ne bi to licilo na navodjenje do resenja celog zadatka onda dati malo veci broj mogucih i slicnih resenja.
Mozda dozvoliti kompletan laptop sa svim i svacim, zbog samo ove namere, bi bilo isuvise.

I po mom misljenji i kad resimo da dozvolimo i kad resimo da ne dozvolimo nesto to mora imati svoj smisao tj. moramo tacno znati zasto i sa kojom namerom smo nesto dozvolili ili nismo dozvolili. Pedagoski pristup i korektnost se ne moze nauciti tek tako kao neki ispit, covek ili ima osecaj za tako nesto ili nema, otprilike nesto kao i talenat.

I kao sto si napomenuo, kad znamo sta je cilj nastave i definisemo plan, udarimo po kriterijumima pa onda muski po tabli i tek na kraju po studentima. Obrnuto bi bilo potpuno nekorektno.

Ok, to je cini mi se nesto drugo. Pitanje je da li je dozvoljeno izloziti teoremu bez dokaza? Pa slozio bi se da je to ok, zaista je besmisleno, posebno ako je nesto korisno, a radi se o prevelikom dokazu. U izlozenom slucaju, sudent racunarstva koristi rezultate druge grane matematike. Pa, sto se mene tice, student racunarstva ne mora da zna nijedan dokaz :) Mislim, za sta mi osposobljavamo tog coveka? Da dokazuje teoreme ili da pravi programe? A student teorijske matematike? Pa on bi valjda trebao da zna vecinu, to mu je zanat... Ne zato sto ce mu znaciti dokazi da bi izveo iz njih nesto drugo, nego bas zato da bi stekao generalno iskustvo, koje ce mu pomoci da sam dodje do ideje za nesto drugo. Moze da mu padne na pamet: hej pa ovde mogu da iskoristim foru iz tog i tog dokaza...

Mislim, generalno ja jesam za taj pristup: ok, cime ces da se bavis? aha, pa onda treba da prodjes ovo. I dva principa: 1. ovo ti treba jer ti treba; 2. ovo ti treba jer razvija sposobnosti koje ce ti pomoci.

Nisam siguran na koju konkretno misliš da sam je pominjao, ali ima više takvih primera. Iz teorije brojeva tu spadaju, recimo, teorema Erdeša i Selfridža (da proizvod nekoliko uzastopnih prirodnih brojeva ne može biti potpun stepen), asimptotska procena za 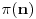i 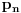, Bertranov postulat, Dirihleova teorema o prostim brojevima u aritmetičkoj progresiji, teorema Grina i Taoa o prostim brojevima u aritmetičkoj progresiji, tehnika rešavanja Pelovih jednačina preko verižnih razlomaka, velika Fermaova teorema (što mi je omiljeno od nabrojanih stvari), i možda još neka dva-tri primera kojih se trenutno ne mogu setiti. Iz geometrije ima (očekivano) dosta manje sličnih primera, ali i tu recimo ne dokazujem da svaka poligonalna linija (bez tačaka samopresecanja) deli ravan na tačno dve oblasti, od kojih je tačno jedna ograničena; kažem studentima da to uzmu kao takvo (i u ovom slučaju stvarno nemaju problema da mi poveruju, jedino imaju problema da shvate zašto ja uopšte pričam bilo šta o tome, kad je to „očigledno“ :)). Pritom, ovde sam navodio samo stvari koje se pominju bilo na predavanjima, bilo na vežbama (a uglavnom na oba mesta), i za koje, imajući to u vidu, smatram da imam pravo tražiti ih na kolokvijumu/pismenom ispitu (primenu, ne dokaz). Činjenica da sam ovde nabrojao, dakle, samo stvari koje se pominju na nastavi, ne isključuje mogućnost da student uradi neki zadatak na drugi način od onog koji sam zamislio (pri čemu se moje zamišljeno rešenje oslanja, naravno, isključivo na gradivo s predavanja/vežbi), i da tom prilikom iskoristi neku teoremu koja nije pomenuta tokom nastave (moguće i neku čiji dokaz zauzima trocifren broj strana); u tom slučaju dobio bi maksimalan broj bodova, pod uslovom da me uveri da stvarno zna da je takva teorema dokazana u literaturi (dakle: ako teorema ima neko ime, može je navesti po imenu; ako pak nema ime, može navesti referencu gde se ona može pronaći).

Još jedna stvar koju takođe aktivno pominjem jesu problemi koji su trenutno otvoreni. Drugim rečima, na vežbama i kolokvijumima viđeni su zadaci tipa „pod pretpostavkom da važi Goldbahova hipoteza, dokazati...“, ili „naći vrednost tog-i-tog parametra takvu da ta-i-ta hipoteza (formulisana u zavisnosti od dotičnog parametra) bude ekvivalentna hipotezi o prostim blizancima“. Smatram da je dobro praviti ovakve konekcije sa savremenim tokovima teorije brojeva (jasno, u onolikoj meri koliku dopušta nivo predmeta na osnovnim studijama).


Imao sam u glavi nešto veće svote za jedan takav laptop, i prilično sam iznenađen tvojom tvrdnjom da je 70 € dovoljno (no nema potrebe da navodiš dokaze, verujem ti, samo prosto nisam očekivao). No, ako uzmemo da bi trebalo nabaviti recimo 100 komada takvih laptopova, to onda izađe 7000 €, što je opet svota koja nije basnoslovna za fakultet, ali ja prosto nemam osnova da od fakulteta tražim tih 7000 € samo za sebe i svoje ispite (primeti da — budući da sam, koliko mi je poznato, jedini koji sprovodi čak i ovu praksu s papirnom literaturom — možemo uzeti kao izvesno da niko osim mene ni te laptopove neće koristiti). (Da napomenem još i to da nisam nikada imao problema s rukovodstvom šta god sam tražio da se nabavi za nastavu i sl., ali je verovatno fazon upravo u tome što, kad god sam mislio da bi nešto bilo dobro da se nabavi, prvo sam procenio koliko je to smisleno tražiti; ovo nikako nije smisleno, bar dok je raspodela stavova povodom korišćenja literature na ispitima ovakva kakva je trenutno.)


A kako tačno misliš da se odredi šta je „potrebno“? :) Nešto tipa da predmetni profesor na nekoliko stranica napravi kompilaciju onoga što je „potrebno“, to podeli studentima, i kaže da smeju kod sebe imati te papire i ništa više? Može, u teoriji izgleda lepo, ali u praksi ruku u vatru stavljam da će se naći bar jedan student kome će smetati što baš te-i-te formule/teoreme nema na papirima (znači, bukvalno šta god da na njima piše, nekome će nešto zafaliti :)). Nije li zato jednostavnije dozvoliti da svako sebi proceni šta će mu trebati, i to i ponese?


Taman posla, naopako bilo da se da nešto što nije obrađivano, ili da formulacija bude namerno iskomplikovana. A što se tiče lažne sigurnosti, poenta je upravo u tome da ne treba nositi od literature nešto u čemu ne znaš šta piše, u nadi da ćeš se na licu mesta upoznati s teoremama odatle, u slučaju da ti zatrebaju (!). Takav pristup osuđen je na propast, i (žao mi je što to moram ovako grubo reći): ako neko padne dva-tri puta, a i dalje ne uspeva da ukapira kako mu je totalno pogrešna koncepcija da na samom ispitu lista nešto što prethodno nije prelistao kod kuće — onda je sam kriv što je postao žrtva te pomenute lažne sigurnosti. I mogu ti reći da studenti koje tokom nastave zapazim kao dobre najčešće ili na ispit ne nose apsolutno ništa, ili eventualno ponesu svoju svesku s vežbi, da im se nađe za svaki slučaj.

A uzmimo sada da je neko čitao i neku literaturu sa strane, u želji da produbi znanje stečeno tokom nastave, pa je pronašao neke teoreme za koje mu se čini da bi možda mogle „jeftinije“ rešiti neke zadatke iz određene tematike obrađivane na predavanjima i vežbama, no nema vremena/volje/želje da pamti sve te teoreme koje je pronašao, da pamti sve uslove koji moraju biti ispunjeni da bi se neka od tih teorema primenjivala i sl. Treba li njega obeshrabrivati povodom takvog vida produbljivanja znanja? Pa jasno da ne (čak upravo suprotno!). Njemu treba omogućiti da, ako zna da postoji „neka slična“ teorema, onda može na licu mesta proveriti kako tačno glasi i da li mu stvarno može pomoći u dotičnoj situaciji. A ako neko nema blage veze šta sve postoji u nekoj knjižurini za koju mu je kolegin kolega rekao da „u njoj ima sve“, pa očekuje da će na licu mesta pronaći nešto što se može iskoristiti — e jbg., nadamo se da će brzo shvatiti da tako ne ide.


Slažem se samo delimično. Tačno je da taj tvoj student treba da stekne to generalno iskustvo, treba da bude u stanju da se seti fore iz tog-i-tog dokaza — ali potreba za time mora mu se demonstrirati upravo kroz žive zadatke, da se on lično uveri kako fora iz tog-i-tog dokaza može biti korisna i na nekom drugom mestu. Možeš ti i celog semestra dogmatski ponavljati neko trabunjanje o generalnom iskustvu i o korisnosti fore iz tog-i-tog dokaza, ali to neće imati nikakvog efekta (bar ne pozitivnog!) ako se studentu ne predoči potreba za time na nekom živom primeru. A pritom postoje stvari koje zaista nisu predviđene da se ikada u životu uče napamet (tipa, neki izrazito tehnički uslovi neke teoreme), koje će čak i najbolji studenti zaboraviti onog momenta izađu iz amfiteatra (i kada im u nekom momentu života, u istraživačkoj karijeri, zatrebaju ti uslovi, najprirodnije će otvoriti knjigu i proveriti kako tačno glase), a tokom tri sata trajanja ispita biće koncentrisaniji na to da im iz glava ne ispari kako glase dotični uslovi, umesto da mogu svu koncentraciju uložiti na rešavanje zadataka. Ne mislim da je to pravi način rada.

Pa otprilike tako nekako. A kompilacija moze imati onoliko strana koliko se smatra da je potrebno. Profesori obicno napisu i svoju knjigu u kojoj bi po prirodi stvari trebalo da bude ono sto treba na ispitu. Na kraju a ko moze bolje od ispitivaca da zna sta ce to pasti na ispitu pa shodno tome on najbolje i zna sta treba staviti u kompilaciju a da ona bude stvarno od koristi. A nezadovoljnih uvek je bilo i uvek ce biti ...

Kada sam mislio na ogranicavanje literature vise sam mislio na zadatke radjene na vezbama i predavanjima jer bi po nekoj mojoj logici barem 1 ili 2 zadatka trebala biti dosta slicna sa onim sto je u tim materijalima pa ne bi bilo fer da neko ponese to i uz malo srece "ubode" nesto sto je blizu 6-ice, kada govorimo o pismenom delu ispita.

Ali, ako pricamo o neogranicenom koriscenju literature na ispitima mozda je interesantniji deo koji se desava ili ce se desiti kada i kod nas sire zazivi sistem "obrazovanja na daljinu" u odnosu na klasicni sistem, i tada "moj sistem" rezonovanja kriterijuma za ispit pada u vodu.
Neki univerziteti u svetu vec imaju u ponudi ovakav sistem obrazovanja, i nisam upoznat sa detaljima da li je tako dobijena diploma ravnopravna ali ogranicenja u tom sistemu mogu biti daleko manje restriktivna nego u klasicnom sistemu gde ipak mozemo imati jak stepen kontrole.

Mozda s ovim pitanjima sirim temu suvise ali smatram da se koncepti vezani za ispite mogu uspesno koristiti u oba sistema.
Bolje je biti pripremljen na tranziciju nego zatecen
Jedino ostaje veliko pitanje da li smo kao rezultat ispita dobili, u sistemu obrazovanja na daljinu, znanje pojedinca ili grupe i da li je to individualna ili grupna diploma

U svakom slucaju o ovome se treba pisati, treba diskutovati, skupljti prakticna iskustva jer ce sigurno biti dobrih, a verovatno jos vise losih predloga, ali iz svega se sigurno moze dobiti neki pozitivan rezultat. Mogucnosti komunikacija, sistemi ali i nacin i tempo zivota su dostigli nivo kada ce u bliskoj buducnosti obrazovanje na daljinu verovatno biti neminovnost. I verovatno nam buducnost donosi manje apsolutnog znanja pojedinca a vise ucenje nacina da se iskoriste mrezni i softverski resursi za dolazenje do resenja.

igorpet

Što se tiče zadatka koji su jako slični zadatku koji je rađen na vežbama, na taj način se na ispitu proverava (skoro) neupotrebljivo znanje, osim ako je taj zadatak nešto što će se posle studija tipičo pojavljivati. Dakle, Bojan i ja zastupamo stav o prenošenju i traženju upotrebljivog znanja.

Na kraju, u tom slučaju bi izrada zadataka bila brža, pa bi student tokom četiri sata mogao da uradi veći broj zadataka, što otvara mogućnost za bolje pokrivanje gradiva zadacima.


Bojane,

Mislim da se stone zadovoljavajuće mašine mogu nabaviti po toj ceni, ali nisam sasvim siguran, jer me takve mašine odavno ne zanimaju. Već skoro pet godina nemam stoni računar. Za sebe kupujem isključivo nove laptopove u rangu cene od oko 500 evra u trenutku kupovine i u tom periodu sam kupio već tri za sebe. No, imam prijatelja koji valja polovnu robu i pouzdano znam da je tržišna cena zadovoljavajućeg laptopa za pokretanje velike većine programa (isključuju se programi kao što su AutoCAD i Photoshop, koje takođe mogu da pokrenu, ali ne na nivou profesionalne upotrebe, a igranje najnovijih hitova je potpuno nemoguće) u naredne dve do tri godine iznosi 100 evra.

No, nisam ja ni mislio da sad tebe naložim da zapucaš u dekanat, već da se razgovara o ovakvoj ideji koliko je dobra, da se širi ako je dobra, pa ako se jednog dana formira kritična masa koja je prihvata, zašto da ne. Međutim, fundamentalan problem su predavači koji svoj predmet ne znaju dovoljno dobro, tj. koji uglavnom znaju da izračunaju samo ono što može i mašina.

Jedan poznanik koji je završio ETF u BG mi je pričao o svom ispitu iz elektronike kod čuvenog profesora Caje. Ispit je bio noćna mora zato što u Cajinom udžbeniku nema skoro ničega opšteg, nego gomile rešenih primera, pri čemu se ideje rešenja ne mogu primeniti nigde drugde ili nije jasno gde i kako. Na stranu što ima i dosta grešaka, za koje ne smatram da treba da budu nepremostiv problem. Onda je našao neku američku knjigu u kojoj je objašnjeno kako se rešavaju zadaci iz elektronike i gle, položio je ispit kod Caje, a da ga nije ni osetio. A dotle, svaki ispitno rok, nauka bato. E, u tome je problem.

Da li to znaci da se na vezbama uglavnom rade zadaci koji daju neupotrebljivo znanje? Ako je tako onda si u pravu.
Ali moje pitanje je onda zasto je to tako, zasto se na vezbama ne rade kvalitetniji zadaci.

Ako mislis da je bespredmetno davati na ispit nesto sto je vec radjeno i obradjeno onda mislim da nisi u pravu jer ako se na vezbama i predavanjima osim elementarnih i uvodnih rade i kvalitetniji primeri zadataka zasto bi onda bilo lose davati takve ili slicne zadatke.
Ako je cilj predmeta ili materije sticanje upotrebljivog znanja onda neka sve bude u tom pravcu pa i ispitni zadaci, ako je vec takav koncept.

Kakve su vežbe, to zavisi od toga ko ih drži i kome. Može na vežbama da se uradi hiljadu najkvalitetnijih zadataka, ali malo je verovatno da će se u praksi tipično sretati zadaci koji su vrlo slični nekom od tih hiljadu zadataka. Na vežbama student treba da se osposobi za rešavanje što više problema, a ne za rešavanje tih hiljadu koji su rađeni na vežbama. Dakle, to je ona priča o profesoru Caji sa ETF-a. On je naučio studente da reše sto zadataka, ali ih nije naučio elektroniku, dok ona američka knjiga uči čitaoca elektronici, a ne rešavanju zadataka iz knjige. Znači, daje u ruke alat za rešavanje široke klase zadataka. Naravno, visokoobrazovan čovek ne treba da zna da rešava samo potpuno šablonske zadatke, već i da razmišlja, koliko-toliko. Ne mislim da zadaci treba da budu za olimpijadu, ali da proveravaju upotrebljivo znanje.

Pa upravo iz tih razloga imamo lose, dobre i odlicne porfesore. Zadaci trebaju da demonstriraju upotrebljivost predmeta, bilo da su zadaci sa ispita bilo da su zadaci sa vezbi. Deluje mi da ti razdvajas zadatke na ispitne i one koji se rade na vezbama. Po meni i ispitni zadaci bi trebali biti koncepcijski i tezinski u skladu sa zadacima na vezbama, osim za visoke ocene gde se malo "dublje" proverava poznavanje materije.

Kazes da ispitni zadaci mozda ne bi trebalo da budu bas olimpijski ali da proveravaju znanje. Ja mislim da bas svi zadaci proveravaju znanje samo sto neki elementarni proveravaju elementarno a takmicarski vrlo visoko znanje. A ocena treba da bude neko objektivno merilo stecenog znanja, 6-ica otprilike znaci elementarno i deo srednjeg znanja a u nekoj gradaciji 10-ka bi trebala da znaci jako visoko znanje, ali to oko 10-ke mi nije bilo nikad bas najjasnije, imao sam ih imao nekoliko, jer licno nisam smatrao da bas briljiram tom materijom iako sam dobro pripremljen izasao na ispit ali u okviru potpuno standardne literature, deluje mi da za 10 treba otici malo dalje sa literaturom i znanjima, ali to je ta sarolikost u kriterijumima.

I ja sam zavrsio ETF, nisam imao cast da licno upoznam Caju jer nisam studirao na Beogradskom univerzitetu, ali bilo je i kod mene par profesora koji su imali da kazemo malo cudne kriterijume, po mom skromnom misljenju, mada licno nikad nisam imao problema sa ispitima i profesorima i ni jedan ispit nisam polagao vise od 3 puta. Ali licni utisci studenata o profesorima nisu uvek bas najmerodavniji, a narocito dok ne poloze taj ispit. Sa neke distance, posle zavrsetka fakulteta, moze da se napravi mnogo bolja i kvalitetnija komparacija predavaca.

U nekom pedagoskom smislu, kad sa ove 12-togodisnje distance pogledam, profesori koji su imali visoko apsolutno znanje i bili "duboko" u materiji su cesce (mada ne i obavezno) losije stojali sa pristupom u objasnjavanju materije a narocito zadataka jer su uvek nesto podrazumevali, isli nekim precicama i bilo je tesko ispratiti ih na casovima. Valjda kad znas mnogo oni elementarni zadaci ti deluju potpuno smesno, oni iz srednje kategorije nedovoljno ozbiljno pa su uvek, cini mi se, imali problem da pogode tezinu ispitnih zadataka, na "stetu" studenata. A studenti ko studenti ... kako god bilo, losim studentima je uvek kriv predavac, oni bolji i odlicni mogu nesto bolje da oforme kriterijum ali uvek je bilo: pa kako mi nije dao 10 a sve sam znao ...

Ja mislim da ti profesori za koje smatraš da su imali "duboko znanje" zapravo nisu imali pojma. To je na primer Caja. On je bio klikeraš da reši razne slučajeve nekim svojim dosetkama, ali nije imao znanje o opšttem u elektronici, pa stoga nije mogao ni da ga prenese. E, onda kada studenti vide kako je on rešio sto zadataka dosetkama, pomisle "ala je ovaj pametan. Kakav genije", a u stvari je suština u tome da on nije imao opšte znanje elektronike, pa je knjiga ispala takva. Caja bi sa tim svojim dosetkama bio verovatno odličan inženjer, ali za profesora treba mnogo više od toga.

Takođe, pravi genijalci ne vide nikakav izazov u rešavanju ispitnih zadataka, niti osećaju potrebu da se prave pametni pred studentima. Takav kompleks obično imaju oni koji su tanki sa znanjem, a ispasti pametan pred studentima je najmanji problem.

Pa bilo je onih koji su imali i realno znanje, za konkretnog profesora koga pominjes ne znam tacno pa ne mogu nista ni da kazem.
Ali hteo sam da kazem da neko ko mnogo zna ne oseca potrebu da se bavi nekim osnovnim stvarima u zadacima ili to jednostavno preskace jer je po njemu to potpuno ocigledno. Nesto sto je za njega ocigledno za vecinu studenata nije i kad ti neko uradi zadatak u 10 redova jer podrazumeva ostalih 50 onda se nadjes u problemu. Ne pricam samo o ispitnim zadacima nego i o onim sa predavanja, vezbi i slicno.
I ne govorim o nekim "demonstracijama znanja" predavaca nego o obicnim predavanjima i izlaganjima.

Ja razumem da on nema motiv da se bavi tim, za njega sitnim i potpuno ociglednim stavarima, ali izmedju motiva i obaveze ja bih ipak bio za to da je predavac tu zbog studenta i da njega nesto nauci. Ko sto kaze ona narodna: Nije znanje znati vec je znanje znanje drugom dati. I uvek je teze drugog nesto nauciti nego sam shvatiti, ako je taj drugi po znanju dosta "ispod" tebe. I profesorski zanat obicno ne podrazumeva samo znanje vec i dosta vise od toga, da uspes da postepeno i jasno uvodis nekog u materiju, da ides od ociglednog ka manje ociglednim, da izbor zadataka bude takav da se postepeno i sistematski ulazi u problematiku, da "se spustis" na nivo studenta i shvatis sta to njemu nije jasno i da to objasnis i kad te niko nista ne pita, da na osnovu iskustva i gresaka studenata sistematizujes neku oblast sa akcentima na tim "problemima- cakama" i jos mnogo toga. Npr. to sto studenti zovu "caka" obicno je samo manje ocigledna i potpuno normalna stvar za predavaca u zadatku ili nekog ko ima iskustva sa tim.

To je skoro uvek mnogo napornije i teze nego jednostavno resiti neki konkretan problem-zadatak. Retki su oni koji sve to mogu bez nekog velikog talenta i sklonosti ka tome. Ostali moraju imati dosta volje i voleti svoj poziv da bi stigli do tog nivoa.

Težište rasprave je skrenulo na unapređenje ispitnih metoda.
Treba dozvoliti korištenje literature.U moje vrijeme to je rađeno prešutno.Svi smo pravili sitno ispisane puškice, šalabahtere ,harmonike...
Tu bi zapisali neke osnovne formule,rutine i sl.Redovno su profesori i asistenti na to gledalo kroz prste,sem rijetkih policijski orjentiranih.
Dakle umjesto puškica studenti bi mogli napraviti solidnu podlogu,ekstrakt iz predavanja,umjesto da to nauče napamet.Individualno pravljenje ovih papira je od velike koristi za savlađivanje gradiva.Naravno da će biti lijenština koji će koristiti tuđe podloge,uglavnom bezuspješno.
Računari na ispitu - NE!Kao ni šestar-lenjir-trokut,ni log.tablice,ni log.računaljka-šiber,ni kalkulator ili neki drugi alati. Ali treba obavezno uvesti kolokvijum rješavanja zadataka na računarima sa bar jednim mat.programom.I to kao uslov izlaska na ispit.
Ne treba škrtariti sa najvećom ocjenom (10).Slučajni lapsus,greška zbog vremenske stiske i sl treba tolerisati.Ali za 6 treba pažljivo odvagati.

igorpet

Najbolji su oni univerziteti na kojima se stekne najveće znanje, pa ti vidi ko predaje na vrhunskim univerzitetima. Sve sam naučni krem iz svojih oblasti. Po tvojoj teoriji bi ti univerziteti bili najgori.


zzzz

Ne radi se samo o ispitnim metodama, već i o ciljevima nastave. Dakle, o tome kakvo znanje treba prenositi i šta je to upotrebljivo znanje. Kalkulator će mi reći da je ln(2)=0.693... Do tog sam rezultata mogao doći i razvojem logaritma u Tejlorov razvoj u okolini tačke 1, pa računanjem logaritma u tački 1/2 i na kraju promenom znaka. Ali, čemu sve to? Naravno da treba znati koristiti Tejlorov razvoj, ali onda neka zadatak bude odgovarajući. Čemu će na kraju meni služiti moje znanje računanja logaritma na ruke? Ako znam da koristim Tejlorov razvoj, ja ću to svakako znati. No, ima i drugih načina da se proveri sposobnost upotrebe Tejlorovog razvoja. Ako profesor ne zna da smisli takve zadatke, onda on ne zna čemu služi Tejlorov razvoj.

Evo, recimo, svojevremeno sam na ispitu iz kompleksne analize imao zadatak da odredim sve kompleksne diferencijabilne funkcije 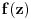na otvorenom jediničnom disku za koje postoji prirodan broj takav da za svako 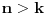važi 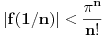. Lepo se zna da su sve diferencijabilne kompleksne funkcije kompleksne promenljive sa otvorenim domenom analitičke, tj. da su beskonačno diferencijabilne i da njihov Tejlorov razvoj u okolini bilo koje tačke konvergira u nekoj okolini te tačke baš toj funkciji, napiše se funkcija u obliku stepenog reda koji je konvergentan ka njoj u nekoj okolini nule, ako funkcija nije nula, postoji prvi koeficijent Maklorenovog razvoja koji nije nula, pa postoje ceo broj 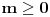i neprekidna funkcija 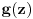takve da je 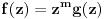i 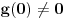, ali onda nejednakost iz zadatka ne može da važi za beskonačno mnogo prirodnih brojeva i gotovo - jedina funkcija koja ispunjava uslove zadatka je nula funkcija. Mala varijacija ideje dokaza teoreme jedinosti. To je primer ne preteškog zadatka zadatak koji provereva sposobnost primene Tejlorove teoreme iz kompleksne analize.

U takvom zadatku ti nikakav kompjuter ne bi pomogao. No, mogući su i zadaci u kojima bi ti kompjuter pomogao ako znaš ono što zadatak proverava.

Vrhunske svetske univerzitete pohadjaju obicno studenti koji imaju odlicna predznanja, tamo prosecni i ispodprosecni djaci ne mogu da stignu, sto zbog materijalnih a sto zbog intelektualnih mogucnosti.
Takvi studenti obicno imaju znanja na samom startu mnogo vise od prosecnih koji dodju do sredine studija.
Studenti koji upisuju te fakultete su sposobni da prate predavanja tih profesora jer imaju jako predznanje steceno na raznim pripremam, takmicenjima i sl.

Npr. mislis li da ce Teodor fon Burg imati problema da proprati bilo koje predavanje vezano za matematiku na bilo kom fakultetu?
Taj i slican nivo znanja upisuje te univerzitete koje spominjes i daleko je to od nekog proseka pa i nije bas za poredjenje.
A mozda i ti profesori shvataju svoju ulogu pa se malo vise potrude i kad im nije do toga, a na kraju krajeva motivisanu su prilicno jer njihovi godisnji prihodi se mere stotinama hiljada dolara za tu ulogu koju imaju u obrazovanju.
A eto npr. Bojan ti moze reci koliko je on "motivisan" od strane drzave ili univerziteta za ono sto radi. Kod nas je uglavnom sve prepusteno licnom entuzijajzmu, sposobnostima i mozda zeljama gde se licni interes stavlja u drugom planu. Ali zato nemamo puno kadrova koji su spremni za sve to.

Po mojoj teoriji kad bi vrhunski univerziteti placali svoje profesore koliko i nasa drzava, kad bi radili u slicnim uslovima i kad bi politika i nacin upisa bila slicna nasem mislim da bi bili duplo gori po rezultatima od nasih univerziteta.

A ja imam drugare koji nisu Teodori fon Burgovi, a doktorirali su na mnooogo boljim mestima od bilo kog srpskog.

Najveći problem je kad nemaš šta da preneseš.

Mi imamo odlicne pojedince, sposobne, radne, sa visokim intelektom i oni bi mogli podici kvalitet brzinom svetlosti ali sta nemamo ... nemamo sistem koji ce stati iza njih, nemamo ekonomiju koja bi ih podrzala i privredu i institute koji bi ih uposlilili i iskoristili u intelektualnom smislu.
O motivima studenata za studiranjem i profesora za predavanjem i sta ciniti posle sudija pricali smo jednom u nekim diskusijama, mislim da se nista nije promenilo niti ce skorije.

Ali sve ovo nije razlog da se pojedinci ne trude da rade najbolje sto mogu i kako mogu, i da ne unapredjuju nastavu, ali valjda je potpuno jasno zasto su oni u velikoj manjini.

Ne. Pre bih rekla da ti on i njegove kolege mogu reći sa koliko entuzijazma se može raditi sa studentima kakvi se ovih godina upisuju na fakultet. Doduše, i to je sistemska greška - fakulteti su plaćeni po broju studenata, pa onda traže način da ih privuku i zadrže i naprave kakvu-takvu normalnu prolaznost... ali sve to prežvakano je na temi "Kuda ide današnje obrazovanje?"

Postovani profesori.

Iz mog iskustva kazem da ostavite studente da sve rade rucno. Dajte manji broj zadataka, ali ono sto rade neka rade rucno. Necete dobiti nista od "pameti" ako u medjuvremenu studenti izgube osnove.

Nakon faksa nisam uzeo olovku u ruke dok sestricina nije krenula u srednju skolu. Sada, nakon 15 godina mi je trebalo mesec dana da udjem u fazon integrala i nizova koje sam resavao zmureci.
Sramota je reci da mi je trebalo 2-3 dana da se podsetim osnovne skole i "rastavljanja na proste cinioce" i deljenja brojeva "bez digitrona".

Moja keva je izasla u penziju pre godinu dana kao profesor matematike. Vi koji radite sa brojevima svaki dan, lako se snalazite, ali budite sigurni da sve veoma brzo bledi...
A ja sam se iznenadio koliko je sve izbledelo...

zivanicd

A da li ti je smetalo u životu to što nisi znao rastavljanje na činioce ili da računaš integrale na ruke? Ja ne znam čime se baviš, ali očigledno da ti nisu trebali integrali.

Onaj kome trebaju integrali, neka lepo nauči da ih koristi, da prepoznaje šta mu treba u datoj situaciji i kako to da upotrebi. U svakom slučaju mu neće izbledeti znanje koje zaista bude koristio, a za ostalo ionako nema veze.

Naravno, ova priča se ne odnosi na uzrast od 7 do 12 godina, već na fakultete. Pedagoški stručnjaci kažu da u tom periodu treba zadavati probleme koji se rešavaju na cake, ali elementarnim sredstvima, a ne debelim teorijama i koji imaju što jednostavniju formulaciju zbog razvoja saznajnih sposobnosti. No, posle 12 godina mozak je prošao kroz tu fazu razvoja.

Osim toga, nema ama baš nikakve nikakve pameti u računanju kvadratnog korena na ruke. Ko je razumeo numeričku matematiku će to svakako znati da uradi na više načina, ali na vežbama i ispitu ne treba da radi zadatke za zaglupljivanje.

Dosta toga diktiraju globalni trendovi.Nisam upućen,ali pretpostavljam da je razvoj matematike dosta slobodan.Šta će od novih stvari ući u programe nastave,a šta će biti izbačeno ili redukovano,ne znam?
Ali znam ovo:Za razliku od školovanja predavača matematike,studiji na tehničkim naukama moraju se brzo prilagođavati novim tehnikama.
Dobri matematički programi na računarima treba da redukuju uvježbavanje silnih zadataka.Naprimjer ja sam imao integrale cijeli semestar (6+4).To bi sad trebalo ići na pola ili još manje,a umjesto toga nešto korisno.Fakulteti (profesori) su tromi,treba im dosta vremena da se prešaltaju.To treba ubrzati.

@bojan

Ne razumem kako si shvatio da ja zelim da se studentima dogmatski ponavlja trabunjanje? :) Stvarno svasta... Ja sam samo rekao da je korisno da zna puno dokaza, jer ih moze kasnije iskoristiti. Isto kao sto mu je korisno da zna da sabira...



Bas ono o cemu sam pricao.

_{[Ovu poruku je menjao darkosos dana 17.06.2012. u 10:41 GMT+1]}

I da, naravno da se stecenom znanju najbolje daje smisao kroz konkretan problem (ne mora bas zivotni :), jer student tada ima osecaj vrednosti svog znanja. Da ne kazem da se ponavljanjem/koriscenjem utvrdjuje znanje. Ali to je vec drugi problem, koji sada ima veze sa odnosom profesor-asistent (makar je tako bilo u moje vreme). Ovaj ti prica jedno na predavanjima, ovaj ti radi 6te zadatke na vezbama. Ne znam ja i sada mislim da je bilo dobro sto je recimo profesor Linearne Algebre nama drzao i predavanja i vezbe. Mada je mnoge nerviralo to sto je prolazio pored svakog, gledao sta radi, kao u srednjoj skoli :) Ali verujem da se dobar odnos predavanja/vezbe moze napraviti i sa dve (razlicite) osobe :) ako imaju dobru saradnju i slicne poglede na to sta i kako treba da se radi.

Jesi rekao da je korisno da zna puno dokaza jer ih kasnije može iskoristiti, ali sam stekao utisak da si pod time mislio kako te dokaze treba eksplicitno zahtevati. Pominjao si dva moguća principa rada, koji funkcionišu u zavisnosti od toga za šta treba osposobiti studenta, ali oba tvoja principa počinju sa „ovo ti treba jer...“ Tu se ne slažemo. Moj stav je da ih ni na šta ne treba terati da uče, već ih treba pustiti da oni sami shvate kako bez znanja tih dokaza neće umeti da urade zadatke na ispitu (to jest, ako mu treba „ona ideja iz onog dokaza“, neće imati vremena da na samom ispitu iščita — iako mu je sve dostupno! — sve ideje koje su se pojavljivale na predavanjima/vežbama, kako bi prepoznao onu koja mu u datom momentu može pomoći).

Slazem se da u nasem obrazovanju ima previse teorije na racun prakse... To onda dozvoljava studentu da "nabuba" dokaz, na pismenom uradi sablonske zadatke, i mozda dobije konacno i 10 a da nista pametno nije uradio... Ali i tvoj stav je drastican, sada je klatno u suprotnom ekstremu: nijedan dokaz koji ne moze da se primeni na zadatke. Slazem se, hajde da kazemo, za vecinu dokaza. Kao sto sam napisao u prethodnoj poruci, ovo mora biti dobro sinhronizovano izmedju predavaca i onog ko drzi vezbe, tj. radi zadatke.

Prvo, pitanje je sta je plan i program konkretnog kursa? Dakle sigurno postoji neki "cilj" kursa. Svakako da ljudima sa tehnickih fakulteta treba vise prakse, jer ce resavati konkretne probleme, dakle koristiti matematiku kao alat. Ma mozda im ne treba nista od teorije, sto rece Nedeljko, nek' nauce da koriste neke od brojnih matematickih programa.

Ali mislim da student matematike mora imati i deo teorije koji mozda ne moze da se direktno iskoristi u nekom zadatku. To mogu biti neki zaista bitni dokazi. Ili na primer neki koji sadrze neku sjajnu ideju, koji pokazuju lepotu matematike. Ne mogu da se pomirim sa tim da se sve to izbaci samo zato sto ne moze da se napravi zadatak, ili makar ne takav koji moze da se resi za odgovarajuce vreme. I na kraju krajeva - to se kosi sa onim osnovnim u matematici: ako nesto tvrdis, za to moras da imas dokaz. Pa ako tako gledamo, i na pismenom ispitu se trazi, ne neki nacin (mozda indirektno), dokaz da je rezultat taj i taj. Da li ti prihvatas nesto sto napise student, npr. neku formulu, koja nije standardna vec moze da se izvede na licu mesta, a da nema opravdanja, makar recima, da je to tako? Znaci odjednom samo bubne ovo je ovoliko i cao? Dolazak do resenja je nesto kao dokaz, jer mora da prati pravila izvodjenja. Pa i u zivotu, kad neko nesto kaze, trazis dokaz, argument - kao sto i mi ovde pricamo :). Pa onda jedan argument na drugi, pa provera, trazenje kontraprimera i na kraju se svede na licni osecaj iliti veru :) Salim se sad malo, ali poenta je ovo: covek koji se bavi naukom koja je tako koncipirana da trazi formalna opravdanja, tesko moze da prihvati nesto bez tog opravdanja. Slazem se da moze biti onih koje preskacemo iz prakticnih razloga, pa se kaze studentima: imajte malo vere da je to sve ok. Ali recimo, evo ja licno sam zavoleo teorijsku matematiku bas zato sto se za sve daje dokaz. I tu je mozda mesto razilazenja - ja nisam goal-driven orijentisan; znaci pitanje je afiniteta: manje mi znaci to sto resim problem, nego npr. dolazenje do ideje i mozda uopstavanje - trazenje dometa problema.

Dakle, da rezimiram, tvoj (i Nedeljkov) stav da treba uneti zivota u prosvetu podrzavam u potpunosti. Koliko mi se cini, ti si asistent na nekom fakultetu, pa bas zbog toga sto je potrebno da neko malo razdrma tu ucmalost, cak bih dopustio i tvoj radikalni stav :) A klatno ce vec naci svoju, sto bih ja rekao, dinamicnu ravnotezu :)

Još samo kada bi obrazložio po čemu su ti dokazi bitni.

Obrazlozi po cemu nisu :)

EDIT: U stvari, nema sta da obrazlazes. Dokazi u matematici nisu bitni... Profesori su potpuno suvisni, jer bi se na predavanjima samo izlagala veronauka u obliku katahizisa. I onako iskaze teorema mogu studenti da nadju gde bilo.

_{[Ovu poruku je menjao darkosos dana 26.06.2012. u 13:44 GMT+1]}

Diskusija se podize na sledeci nivo, argumenti pljuste sa svih strana jedino se sustina malo slabije nazire

Kakvo pitanje, takav i odgovor :) Sustinu sam izlozio u prethodnoj poruci, ovo je samo imitiranje...

Pa, znaš šta, ako treba nešto učiti, znači da treba izdvojiti vreme i trud za to, a to mora nečim da se opravda, tako da je teret pravdanja na tebi.

Hm, znaci ti hoces da menjas plan i program a ja moram da se pravdam? :) Nemam pojma, argumente sam vec izneo, ne znam sta da dodam... Jednostavno mi princip po kome prikaz dokaza na predavanjima zavisi od toga da li od tog dokaza moze da se sastavi zadatak koji je moguce resiti npr. za sat vremena, ne zvuci dobro. Uostalom, ako si procitao onaj moj duzi post, videces da se slazem da treba da se nesto menja, i to bas u navedenom pravcu, ali princip kojim bi se rukovodili u takvoj redukciji izlaganja dokaza mi se ne svidja.

Ne radi se o tome ko će šta da menja. Zamisli da se otvara nov matematički fakultet. Dakle, nema nikakve programe, tek treba da se donesu. Razumem ja da ti ne prihvataš taj kriterijum bitnosti, ali nisi izneo nijedan drugi. Pitao sam zašto je neki od takvih dokaza bitan, a ti jednostavno nemaš odgovor.

Hm, preuranjeno je da kazes da nemam odgovor (stavise, nekako je negativno), mozes reci da ga nisam izneo, ili da ti to nisi pronasao u tekstu koji sam do sada napisao (iako ja mislim da je trebalo).

Hajde nek' tek treba da se naprave programi. Nisam video koji je tvoj princip izbora? Meni to izgleda ovako: ok, znamo sta je tematika i domet, hajde da vidimo sta imamo od zadataka koji mogu da se rese koristeci to znanje, a koji su prilagodjeni ispitu koji traje toliko, gde imao toliko zadataka; ok, sad imamo zadatke, hajde da vidimo koji su nacini za njihovo resavanje; dobro, shvatili smo sta im treba od teorema, i da je dobro da znaju dokaze tih i tih teorema jer mogu da iskoriste tehniku dokaza te teoreme.

Cak i u slucaju da sve ove tacke prodjes idealno (posebno to sta sve nekom moze da padne na um), ne vidim sta ce tu ostati od dokaza. Dakle, u tom predlogu je mesto predavaca teorije potpuno suvisno. Sve se onda moze uraditi na vezbama... Dakle smer Teorisjka matematika i primene, mozemo da preimenujemo u Primenjena matematika. Ok, slazem se, nek' postoji takav smer, al' ne bih voleo da se ukida ovaj prvi :)

Ne znam koji pristup vise da koristim da bih objasnio svoje glediste... Ali recimo da su ovo kriterijumi:
- dokazi koji pokazuju neku bitnu osobinu objekata o kojima se prica - razlog: da se izgradi intuicija, dakle "osecaj" sa cim mi tu imamo posla
- dokazi koji sadrze neku bitnu tehniku, bez obzira da li ona moze da se ugura u ispitni zadatak - razlog mislim da je jasan, neces uvek resavati zadatke od 1h (od ideje do realizacije)
- dokazi koji treba da "ojacaju veru" - recimo kod nekih neintuitivnih stvari - razlog: pa ako je nesto protivno intuiciji, vera opada a sumnja raste :)

Naravno, ako neki od tih dokaza prevazilaze mogucnost da se pokazu za cas-dva, nek' se preskoce. Ili mogu da se daju u skracenoj formi, samo sa idejom i manjim tehnikalijama.
Vec sam napisao ranije, matematika nije veronauka; i drugo - nije posteno da dajemo bez dokaza, a trazimo sa dokazom; uostalom, kad se vec trazi dokaz, kako student zna kako on treba da izgleda? Na osnovu srednjoskolske predstave? Kako ce razviti stil pisanja dokaza? Sta se moze preskociti, na sta mora da se obrati paznja i slicno?

Mislim da sam shvatio tvoje glediste, posebno nakon one analogije sa programiranjem: daj ljudima alat - koji ne treba da dovode u pitanje - i daj im onda dobro smisljene zadatke koji ce razvijati kreativnost. Pa dobro, ako ce u zivotu samo raditi zadatke, u kojima je bitan samo rezultat, moze i tako.

Ja spadam u one koji nisu štrebali zadatke, pa posle pismenog učili teoriju, jer je meni neshvatljivo kako to može. Tehnika izrade zadataka proističe iz teorije, a ne obrnuto. No, smisao teorije je osposoobljavanje za rešavanje problema.

Da li bi mogao da navedeš primere za ovo? Posebno me zanima koje su to bitne tehnike koje se ne mogu ugurati u zadatke.

Ja spadam u one koji nesto i ne vole zadatke, jer mi je to samo ponavljanje teorije :) A takodje spadam u one koji nikad ne bi studirali matematiku u kojoj se ne prikazuju dokazi. Mozda sam ja jedinstven slucaj, ali za mene je bilo prosvetljenje to sto sam konacno video zasto su stvari takve kakve jesu. I verovatno da nisam studirajuci matematiku dobio te odgovore, okrenuo bi se necemu drugom. To sto bi oni mene obucili da radim zadatke, nije mi zanimljivo, znao sam i pre toga, sada samo u drugim oblastima, i prosirenim alatom. E sad, posto se ne bavim matematikom vec dugo, osim preko ovog foruma, pitanje je sta je bila svrha? Pa, za mene je dovoljno da sam dobio odgovore...

Takodje, izneo sam dosta argumenata, na koje se nisi osvrnuo, a sve je to deo ove price. Sto se tice uguravanja u zadatke, pa za sve moze da se kaze da je zadatak... Pre nego sto je neko nasao dokaz nekog tvrdjenja ili ga uopste formulisao, i to je bio zadatak. Ali mozda nije bio zadatak koji je primeren ispitu, zbog duzine ili tezine. I sta sad? Da li si ti siguran da imas odgovarajuci zadatak za svaku bitnu tehniku? Morali bi prvo da definisemo sta su bitne tehnike, ali to je vec daleko ozbiljnija stvar od ovog dopisivanja. Zato se zadrzavam na opstijoj diskusiji, a tvoje je da, ako zelis ozbiljno da pristupis ovome, napravis spisak.

I sta je sa ostalim mojim argumentima? Uostalom, prilicno je jasno sta zelim da kazem, ko hoce da cuje :) I nemam nameru nesto da se nastavljam, vec sam rekao da ja takvu matematiku ne bih studirao i to je to. Dakle nikad ne bih razvio strogost zakljucivanja (onoliko koliko imam) da nisam video kako se sve to dokazuje. Nikakav gubitak za nauku :)

Dakle, rešavanje zadataka bez razumevanja konteksta nema nikakvog smisla, jer ne može da se primeni. To ti je kao da naučiš algoritme za računske operacije nad nizovima cifara, a onda ne znaš na pijaci da izračunaš koliko košta dva kila jabuka i tri kila krušaka. Tu smo se složili.

Što se izlaganja dokaza u cilju vežbanja zaključivanja tiče, pa dokaza će na nastavi matematike ionako biti preko glave, tako da tu nema brige. Pristalica sam izlaganja jednostavnih dokaza kojima se stvari povezuju.

E, sad, ti kažeš da te je zanimalo zašto važi npr. Stirlingova formula. I mene je zanimalo i produbio sam dokaz koji smo učili (izveo sam mnogo više od onoga što smo učili). To je OK. Ali, vidiš, taj dokaz sadrži opštiju tehniku, koju nismo učili, a trebali smo. Sa druge strane, nikada nismo učili dokaz Cermelove teoreme o dobrom uređenju i Cornove leme, a kasnije sam proučavajući tu problematiku shvatio da i tu ima bitnih tehnika koje se mogu opštije primeniti.

Sa zadovoljenjem znatiželje kao argumentom mogu da se složim, kao i sa time da bi teorijski matematičar trebao da zna zasnivanje matematike, koje se u vreme kada sam ja bio student nije učilo. Savremeno zasnivanje matematike ide preko ZFC teorije skupova zasnovane na predikatskom računu prvog reda.

Međutim, slažeš li se ti da je ostalo pitanje kriterijuma koji su dokazi bitni, a koji ne.

Da, slazem se, naravno. Ja sam samo pokusao da nadjem opste smernice. Na kraju krajeva, ako bismo zeleli da ozbiljno ovu temu razradimo, prakticno bi napravili plan i program kursa :)

E sad, ne znam da li si primetio, ali s' obzirom kako je Bojan izneo svoje glediste, a slozili ste se, ja sam shvatio da zelite da prakticno podredite izlaganje gradiva onome sto ce se raditi kroz zadatke. To bi znacilo izbacivanje svih dokaza koji ne mogu da se iskoriste, sa cim nikako nisam mogao da se slozim. Ako to nije tako, vec samo hoces da izbacis nepotrebno, pretehnicke dokaze bez mnogo vrednosti ili slicno, onda se slazem (posebno sto takvi glomazni dokazi mogu da znace da nije dobro izabran pristup, ali se jos niko nije setio boljeg :).

Ostalo sto si napisao je prakticno kritika sadasnjeg nacina izlaganja gradiva, gde svakako ima mesta za poboljsanje. Ali kao i svuda, nisu uvek pravi ljudi na pravim mestima :)

Dakle, ja ne znam kakav je sadasnji stav u prosveti sto se tice izlaganja dokaza? Ispricati sve? Ili profesori imaju neku autonomiju pristupa?

Ja bih zapravo ukinuo sve smerove i uveo zapadni sistem sa izbornim predmetima. Lepo, postoji predmet "zasnivanje matematike", pa ko hoće, neka ga izabere.