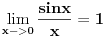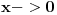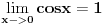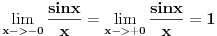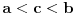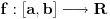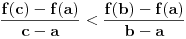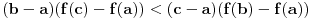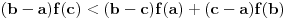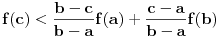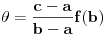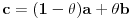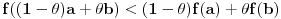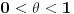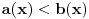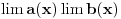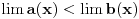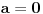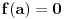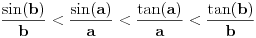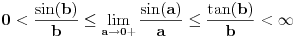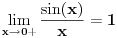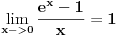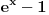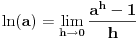[ patkan1992 @ 17.06.2012. 15:55 ] @
|
[ igorpet @ 17.06.2012. 16:46 ] @
Citat: patkan1992: ... Moze neko da mi pomogne oko pocetka dokaza? Ne razumem, postavljanje uslova: "Neka za 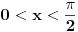 (Ovde je samo manje) vazi (Ovde je samo manje) vazi 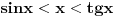 (Ovde je manje-jednako). (Ovde je manje-jednako).Odatle sledi: 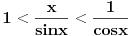 , tj. , tj. 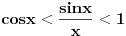 " "Valjda se sa slike bolje uocava:  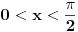 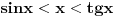  [ zzzz @ 17.06.2012. 16:48 ] @
Nacrtaj trig.kružnicu i neki ugao u prvom kvadrantu.Taj ugao je veći od nula,a manji od 90 stepeni.Sad ucrtaj sin tog ugla.Ta duž je kraća od luka ugla.Ucrtaj duž tangensa tog uglla i vidiš da je duža od luka "x".
Zašto u drugom koraku 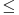 a ne a ne 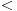 (inače u latexu \le i \ge= 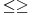 .. vidi http://kokice.striga.org/4.14.html) .. vidi http://kokice.striga.org/4.14.html)Možeš raditi i sa < , pa ćeš na kraju imati nešto ovako kad x teži nuli: 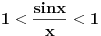 ,(Teži da istovremeno bude i veće i manje od 1 i dođeš do zaključka da se sinus,luk i tangens u graničnom slučaju izjednačuju.Vratiš se nazad i ubaciš i tu mogućnost. ,(Teži da istovremeno bude i veće i manje od 1 i dođeš do zaključka da se sinus,luk i tangens u graničnom slučaju izjednačuju.Vratiš se nazad i ubaciš i tu mogućnost....Vidim da je Igor ubacio crtež.Mislim da ona zelena linija (tgx) djeluje očiglednije kad je okomita u tački 1. [ Nedeljko @ 17.06.2012. 17:02 ] @
Kako ste vi uopšte definisali sinus i broj pi? Van konteksta definicija dokazi nemaju smisla.
[ patkan1992 @ 17.06.2012. 17:13 ] @
Hvala vam!
Nedeljko, nismo definisali... Samo ovako pise, kao sto sam napisao. [ igorpet @ 17.06.2012. 17:26 ] @
Citat: Nedeljko: Kako ste vi uopšte definisali sinus i broj pi? Van konteksta definicija dokazi nemaju smisla. Moze i ovako:  Izvor: Wikipedia-Trigonometrijske funkcije-Granicne vrednosti [ Nedeljko @ 17.06.2012. 18:43 ] @
Ovo je školski primer zašto je pogrešno učiti iz enciklopedije.
Ako se ne zna šta je sinus, onda se ne može reći ni koliki je navedeni limes. Dakle, dokaz se mora suštinski naslanjati na definicije, odnosno od toga kakve su definicije zavisi i kakav je dokaz. Ako u dokazu ovog tabličnog limesa nije bitna definicija sinusa, onda se sinus može zameniti bilo kojom drugom funkcijom. Zašto onda ne bi bilo npr. 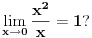 Kada enciklopedija govori o nekom pojmu, normalno je da se navede nekoliko pristupa njegovom uvođenju. Ali, na koju će onda definiciju da se osloni dokaz? Ono što bi bilo izvodljivo je da se dokaže za nekoliko načina uvođenja pojma da su ekvivalentni, tj. da vode ka istom pojmu, pa je onda svejedno na koje će se uvođenje dokaz naslanjati. Međutim, to obično u enciklopedijama nije slučaj. Odakle njima recimo formula da su katete manjeg trougla sin(x) i cos(x)? Šta je tu x? Zašto je površina kružnog isečka x/2? Ova pričica može da prođe na školskom nivou izlaganja matematike, ali svakako nije za ozbiljno zasnivanje matematike. [ Nedeljko @ 17.06.2012. 18:45 ] @
patkan1992
Ako niste definisali sinus, onda nemate šta ni da dokazujete. No, ako profesor traži dokaz za ocenu, budi praktičan i nauči to što je izverglao. [ patkan1992 @ 17.06.2012. 19:01 ] @
Pa 'ajde, koja bi definicija sinusa (i cega jos treba) bila ovde?
[ Sonec @ 17.06.2012. 19:12 ] @
Prikacio sam fajl u kome ima malo vise o trigonometrijskim funkcijama.
Za zipovan fajl (raspakujte ga celoga, nece moci da prikaze ako je samo dvi raspakovan, zbog slika) bice vam potrebam citac Yap (ili neki drugi za .dvi fajlove) koji je sastavni deo instalacije MikTex-a. Ja sam pokusao da ga konvertujem u PDF i ispalo je poprilicno ruzno, tekt je zbijen. Za bolji pregled preporucujem da se gleda sa 200 - 300% uvecanja teksta. EDIT: na pdf cete morati malo da sacekate, jer zbog velicine samoga fajla ne mogu ga uploadovati uz poruku [ Sonec @ 17.06.2012. 20:00 ] @
Evo i pdf fajla: http://www.sendspace.com/file/lx9xet
Takodje, moze se pogledati i ovde http://poincare.matf.bg.ac.rs/~miodrag//kf_pdf.zip Inace, pdf koji sam prilozio je od moga profesora, ja sam to radio, al mislim da kod drugih profesora to nije toliko detaljno radjeno (verovatno zato sto se radi u okviru predmeta Kompleksna analiza). Na primer, kod Adnadjevica i Kadelburga pise da trigonometrijske funkcije 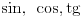 i i 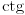 nece posebno defnisati, vec ce podrazumevati da je poznato njihovo uvodjenje pomocu trigonometrijskog kruga. Takodje, pretpostavice da su poznata osnovna svojstva tih funkcija (definisanost, parnost, periodicnost, ogranicenost, monotonost, adicione formule i slicno). Tako da bar u toj knjizi trigonometrijske funkcije nisu tako detaljno uradjene. nece posebno defnisati, vec ce podrazumevati da je poznato njihovo uvodjenje pomocu trigonometrijskog kruga. Takodje, pretpostavice da su poznata osnovna svojstva tih funkcija (definisanost, parnost, periodicnost, ogranicenost, monotonost, adicione formule i slicno). Tako da bar u toj knjizi trigonometrijske funkcije nisu tako detaljno uradjene.[ Nedeljko @ 17.06.2012. 20:59 ] @
Citat: patkan1992: Pa 'ajde, koja bi definicija sinusa (i cega jos treba) bila ovde? Pa, evo ovako: 1. Definisati izometrije ravni i klasifikovati ih. 2. Definisati ugao kao geometrijski pojam (dve poluprave sa zajedničkim temenom dele ravan na dve oblasti itd.), kao i pojam pravog ugla. 3. Definisati pojam zbira susednih uglova. Uglovi su susedni ako imaju jedan zajednički krak i nemaju nijednu zajedničku unutrašnju tačku, a zbir im je ugao čiji su kraci preostala dva kraka i kome pripadaju tačke zajedničkog kraka. 4. Definisati meru ugla kao funkciju koja svakom uglu pridružuje pozitivan realan broj, koja se slaže sa operacijom sabiranja susednih uglova i koja podudarnim uglovima pridružuje isti realan broj. 5. Dokazati da za proizvoljno izabranu meru uglovi imaju istu meru akko su podudarni. 6. Dokazati za svaki pozitivan realan broj a postoji tačno jedna mera uglova kod koje je mera pravog ugla jednaka a. 7. Dokazati da za svaki pozitivan realan broj koji je manji od mere bar jednog ugla postoji ugao čija je taj broj mera. 8. Definisati trigonometrijske funkcije na uglovima (najpre oštrim, a potom i ostalim). 9. Dokazati da su trigonometrijske funkcije podudarnih uglova jednake. 10. Definisati dužinu luka. 11. Definisati broj pi kao odnos obima i prečnika kruga. 12. Definisati površinu npr. kao Žordanovu meru. 13. Izvesti osnovne osobine mere. 14. Dokazati da je figura podudarna figuri merljivoj po Žordanu takođe merljiva po Žordanu i da ima istu Žordanovu meru. 15. Izvesti formulu za površinu kruga. 16. Izvesti formule za dužinu kružnog luka i površinu kružnog isečka. 17. Uvesti meru uglova u kojoj prav ugao ima meru pi/2 kao standardnu i opravdati to najjednostavnijim oblikom formule za dužinu kružnog luka. 18. Uvesti trigonometrijske funkcije pozitivnih realnih brojeva manjih od 2*pi kao trigonometrijske funkcije uglova kojima je to mera. 19. Dokazati da se tako uvedene trigonometrijske funkcije mogu produžiti neprekidno i 2*pi na ceo skup realnih brojeva (barem što se tiče sinusa i kosinusa). E, onda može da prođe ona pričica. [ igorpet @ 17.06.2012. 21:36 ] @
[ Nedeljko @ 17.06.2012. 22:28 ] @
Šta je radijan? To je ona moja priča odozgo.
[ igorpet @ 17.06.2012. 22:40 ] @
Citat: Nedeljko: Šta je radijan? To je ona moja priča odozgo.  Wikipedia-Radijan Trigonometrijske funkcije se obicno definisu preko pravouglog trougla:  Nedeljko, ja mislim da je postavljac teme srednja skola i da su oni vec presli i sta su trigonometrijske funkcije i sta je radijan i trigonometrijska kruznica i dosli su do lekcije gde definisu neke granicne vrednosti ovih f-ja. Verovatno mu konkretan dokaz nije bio jasan, pa je vec prva slika pojasnila dosta toga ... ali sa ovim ostatkom mislim da je kompletiran za nivo srednje skole. [Ovu poruku je menjao igorpet dana 17.06.2012. u 23:50 GMT+1] [Ovu poruku je menjao igorpet dana 17.06.2012. u 23:50 GMT+1] [ Nedeljko @ 17.06.2012. 23:06 ] @
Ne vredi da ti više pišem kad ne čitaš ni napisano.
Pozdrav [ Sonec @ 17.06.2012. 23:15 ] @
Nedeljko je u pravu. Ako hocemo da govorimo o korektnom dokazu onda se on mora zasnivati na definicijama/aksiomama teorije koju posmatramo.
Inace, postavljac teme nije srednjoskolac, ako je verovati ovoj temi http://www.elitesecurity.org/t432343-0. Takodje, smatram da ne bi trebalo previse detaljisati za studente tehnickih fakulteta. [ igorpet @ 17.06.2012. 23:23 ] @
Citat: Sonec: Nedeljko je u pravu. Ako hocemo da govorimo o korektnom dokazu onda se on mora zasnivati na definicijama/aksiomama teorije koju posmatramo. Inace, postavljac teme nije srednjoskolac, ako je verovati ovoj temi http://www.elitesecurity.org/t432343-0. Takodje, smatram da ne bi trebalo previse detaljisati za studente tehnickih fakulteta. OK, mozda je tako najpravilnije ali i ja kao neko ko je zavrsio tehnicki fakultet nemam naviku da od ovakvog dokaza teoreme tablicnog limesa pravim citav naucni rad. [ Nedeljko @ 18.06.2012. 10:12 ] @
igorpet,
Tamo se pominje nekakva "mera ugla". Šta je sad pa to? To je ono o čemu sam pisao u tačkama 3-7. A radijan je ono što sam nappisao u tački 17. Opet se postavlja putanje šta su obim i površina, a to je ono o čemu sam opet pisao u istoj poruci, tako da ne vredi da pišem ako se ne čita ono što sam već napisao. Slažem se ja da ne treba ići u neku duboku filozofiju za studente tehničkih fakulteta, ali čemu onda navođenje "dokaza", kada se ne zna ni šta oni dokazuju? Studentima tehnike ne trebaju ti "dokazi", a ni korektno zasnivanje matematike, već alat. Stoga je odgovor na pitanje kako student tehničkog fakulteta treba da nauči ovakve "dokaze" - onako kako profesor traži. [ zzzz @ 18.06.2012. 13:39 ] @
Citat: Nedeljko:Pa, evo ovako: 1. Definisati izometrije ravni i klasifikovati ih. 2. Definisati ugao kao geometrijski pojam (dve poluprave sa zajedničkim temenom dele ravan na dve oblasti itd.), kao i pojam pravog ugla. 3. Definisati pojam zbira susednih uglova. Uglovi su susedni ako imaju jedan zajednički krak i nemaju nijednu zajedničku unutrašnju tačku, a zbir im je ugao čiji su kraci preostala dva kraka i kome pripadaju tačke zajedničkog kraka. 4. Definisati meru ugla kao funkciju koja svakom uglu pridružuje pozitivan realan broj, koja se slaže sa operacijom sabiranja susednih uglova i koja podudarnim uglovima pridružuje isti realan broj. 5. Dokazati da za proizvoljno izabranu meru uglovi imaju istu meru akko su podudarni. 6. Dokazati za svaki pozitivan realan broj a postoji tačno jedna mera uglova kod koje je mera pravog ugla jednaka a. 7. Dokazati da za svaki pozitivan realan broj koji je manji od mere bar jednog ugla postoji ugao čija je taj broj mera. 8. Definisati trigonometrijske funkcije na uglovima (najpre oštrim, a potom i ostalim). 9. Dokazati da su trigonometrijske funkcije podudarnih uglova jednake. 10. Definisati dužinu luka. 11. Definisati broj pi kao odnos obima i prečnika kruga. 12. Definisati površinu npr. kao Žordanovu meru. 13. Izvesti osnovne osobine mere. 14. Dokazati da je figura podudarna figuri merljivoj po Žordanu takođe merljiva po Žordanu i da ima istu Žordanovu meru. 15. Izvesti formulu za površinu kruga. 16. Izvesti formule za dužinu kružnog luka i površinu kružnog isečka. 17. Uvesti meru uglova u kojoj prav ugao ima meru pi/2 kao standardnu i opravdati to najjednostavnijim oblikom formule za dužinu kružnog luka. 18. Uvesti trigonometrijske funkcije pozitivnih realnih brojeva manjih od 2*pi kao trigonometrijske funkcije uglova kojima je to mera. 19. Dokazati da se tako uvedene trigonometrijske funkcije mogu produžiti neprekidno i 2*pi na ceo skup realnih brojeva (barem što se tiče sinusa i kosinusa). E, onda može da prođe ona pričica. Dakle da bi dokazali da omjer sinusne funkcije i njenog argumenta teži ka jedinici,ako argument teži ka nuli,treba odraditi onih 19 tačaka. I to neposredno prije samog dokazivanja!?I to specijalno baš zato što se namjerava "početi ona pričica!?". Po mojoj procjeni za to treba oko 20 nastavnih časova,a u pisaniom obliku oko 200 strana knjige.I to uz opsežnu pomoć na ukazivanje na literaturu.Bil Nedeljko mogao navesti literaturu gdje je tako urađen ovaj ili dokaz nekog sličnog limesa? Navođenjem u onih 19 tačaka (šta se sve mora definirati) zaboravio Nedjeljko najvažniju stvar:Definisati pojam definicije.Jer bez jasnog objašnjenja tog pojma,kako ćeš se služiti sa njim.Nikako.To jest možeš napisati bilo šta i reći da time definiraš ovo ili ono.Ali da nebi upao u vrtlog filozofskih rasprava,mišljenja sam da se uvjek treba pokušati što racionalnije izraziti.Upućivanjem na literaturu koja obrađuje dati pojam. Naprimjer ja ću ubuduće pri izvođenju spomenutog izvoda,navesti odmah na početku da je neophodno prethodno uraditi [url=mailto:http://www.elitesecurity.org/p3125523]ovo.[/url]Ušteda 20 sati!Ali takođe sam siguran da onaj kome objašnjavam zna šta je ugao,šta pi,radijan,sinx i ostalo.Kako bi došao do limesa,ako nije prošao treći osnovne gdje se uči pojam ugla,ili peti kad se uči šta je to pi? Istina među onih 19 ima i opasnih stvari za koje je potrebno znanje apsolventa na PMF.Iz toga se da zaključiti da dotični izvod i ne može korektno izvesti niti shvatiti gimnazijalac jer nezna naprimjer:"14. Dokazati da je figura podudarna figuri merljivoj po Žordanu takođe merljiva po Žordanu i da ima istu Žordanovu meru."...He he he.. Alaj si ga prećereo oj Neđeljkooo. [ patkan1992 @ 18.06.2012. 14:09 ] @
Uvek je i bilo "radite onako kako vam profesor trazi". Inace, ovih 19. tacaka su uzas. :) Na Saobracajnom fakultetu sam, i ne radimo teoriju ovoliko opsirno (iliti perfektno detaljno :D). Veca koncentracija je na rad zadataka, a usmeni kasnije kako kod koga profesora. Neki manje trazi, neki vise, ali nijedan ne trazi da dokazujemo celu istoriju matematike zbog
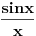 . Samo mi nisu bili jasni ti uslovi, ali sada razumem po slici od iznad. I to ce biti dovoljno za dokaz kod nas. :) . Samo mi nisu bili jasni ti uslovi, ali sada razumem po slici od iznad. I to ce biti dovoljno za dokaz kod nas. :)Nedeljko, tebi svaka cast! :) [ Nedeljko @ 18.06.2012. 14:57 ] @
Citat: zzzz: Dakle da bi dokazali da omjer sinusne funkcije i njenog argumenta teži ka jedinici,ako argument teži ka nuli,treba odraditi onih 19 tačaka. Da bismo dokazali da odnos sinusa i njegovog argumenta teži ka jedinici kada argument teži nuli, moramo prvo znati šta je sinus. Bez toga ispada da isti rezultat važi i ako sinus zamenimo bilo kojom drugom funkcijom, na primer kvadratnom. Citat: zzzz: I to neposredno prije samog dokazivanja!?I to specijalno baš zato što se namjerava "početi ona pričica!?". Ne, već se radi o opštim stvarima koje imaju mnogo širi značaj od te pričice. Citat: zzzz: Po mojoj procjeni za to treba oko 20 nastavnih časova,a u pisaniom obliku oko 200 strana knjige.I to uz opsežnu pomoć na ukazivanje na literaturu.Bil Nedeljko mogao navesti literaturu gdje je tako urađen ovaj ili dokaz nekog sličnog limesa? Procena ti je vrlo loša, a što se literature tiče: A) Tačke 1-7 - "Geometrija" Zorana Lučića. B) Tačke 8-9 su trivijalne na osnovu prethodnog. C) Tačke 11, 13-16 - Matematička analiza I Milosava Marijanovića. D) Tačke 12, 17-19 - trivijalno na osnovu prethodnog. E) Pričica - trivijalno na osnovu prethodnog. Citat: zzzz: Ali takođe sam siguran da onaj kome objašnjavam zna šta je ugao,šta pi,radijan,sinx i ostalo. Zna ili misli da zna ili ti misliš da on zna ili ti misliš da ti znaš šta su ti pojmovi? Citat: zzzz: Kako bi došao do limesa,ako nije prošao treći osnovne gdje se uči pojam ugla,ili peti kad se uči šta je to pi? Pa, tako što im radiš aksiomatski ne pominjući reč "aksioma" uvođenjem stavova koji se ne dokazuju, a do na koje radiš ostalo. Eto, recimo kada smo kod učiteljice radili prirodne brojeve, nije se dokazivalo da su sabiranje i množenje komutativni, ali je učiteljica to svakako rekla i to smo koristili. U školi nismo dokazivali stavove o podudarnosti transverzalnih uglova, uglova sa normalnim kracima itd, ali smo ih učili i koristili. Citat: zzzz: Iz toga se da zaključiti da dotični izvod i ne može korektno izvesti niti shvatiti gimnazijalac jer nezna naprimjer:"14. Dokazati da je figura podudarna figuri merljivoj po Žordanu takođe merljiva po Žordanu i da ima istu Žordanovu meru."...He he he.. Izvesti ne, ali shvatiti da. Vidi moj prethodni pasus. Citat: zzzz: Alaj si ga prećereo oj Neđeljkooo. Nisam preterao ni za milimetar. To stvarno logički prethodi onoj pričici u zasnivanju matematike. I ne samo to, nego ako ćemo mak na konac, predikatski račun prvog reda, ZFC aksiomatska teorija skupova, Peanova aritmetika u njoj i polje realnih brojeva u njoj da bi se stiglo do onih 19 tačaka. Druga je stvar kome treba zasnivanje matematike, a kome samo alat koji razume i zna da koristi. patkan1992 Kada sam pitao kako ste uvodili sinus, nisam hteo da budem destruktivan, već samo da pomognem, a od uvođenja elementarnih pojmova (a ne mora se sve 100% strogo) zavise i elementarni dokazi. Primera radi, moj profesor analize 1 i 2 je definisao sinus na sledeći način: 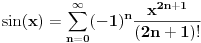 . .Onda je dokazivao osobine tako uvedenog sinusa, gde spada i periodičnost i postojanje najmanjeg pozitivnog rešenja jednačine 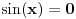 , koje je bilo definicija broja , koje je bilo definicija broja  . U tom slučaju bi dokaz onog tabličnog limesa bio potpuno drugačiji. . U tom slučaju bi dokaz onog tabličnog limesa bio potpuno drugačiji.[ miki069 @ 27.06.2012. 12:06 ] @
U dokazu iz "enciklopedije" piše da je sinus "parna" funkcija, pa je dokaz za negativne X identičan.
Kjučni nedostatak je što je u dokazu korišćena teorema, a nije navedena niti je dokazana. [ miki069 @ 14.04.2023. 17:29 ] @
Bez dokaza ovog limesa nema dokaza da je izvod od sin(x) jednak cos(x).
U toku dokaza je ključna nejednakost: sin(x)<x<tg(x). Ona je dokazana korišćenjem obrasca za površinu kružnog isečka. Ne znam ni jedan dokaz za površinu kruga koji ne koristi limes koji se dokazuje. [ miki069 @ 17.04.2023. 21:24 ] @
Nejednakost sin(x)<x je trivijalna.
Sporna je nejednakost x<tg(x)? Bez tog dokaza je cela Analiza u rekurziji. Sve je OK, a ne valja ništa. [ BrutalCoin @ 18.04.2023. 08:41 ] @
Hoćemo da uredimo matematiku?
Može ali izlaganje matematike se sastoji od ad-hok nabacanih teza. Kako onda? Na primer Adnadjević/Kadelburg "Martematička analiza I" u odeljku "Njutn-Lajbnicova formula" navode teoremu 8.3.2: Citat: Neka je f:[a,b] --> R neprekidna funkcija i Psi proizvoljna njena primitivna funkcija... I iz napisanog se (pogrešno) zaključuje da je primitivna funkcija proizvoljna. Dalje, autori navode Dokaz i pišu: Citat: ... prema prethodnoj teoremi ... Medjutim, prethodna teorema (8.3.1) nema dokaz. Kako neko napisa - "Pričica". Kojim redosledom Mateljević "Kompleksne funkcije 1 & 2" definiše pojmove: 1.5.1. Funkcije cos, sin, cis; Definicija 1.13 (Broj Pi) 3. Definicija ugla. [ Nedeljko @ 21.04.2023. 15:19 ] @
Matematika je vrlo uređena, a to uređenje ima i vrlo egzaktnbu formulaciju.
Neprekidna funkcija na intervalu ima beskonačno mnogo primitivnih funkcija, koje se razlikuju donna aditivnu konstantu. navedeni izraz znači da je Psi primitivna funkcija funkcije f, bez dodatnih pretpostavki. Kada se kaže "za ma koji element skupa A", tu se ne pretpostavlja ni da je skup A neprazan. Naravno da iz uvedene pretpostavke sledi da je skup A neprazan. Međutim, ta pretpostavka se može uvesti bez obzira na to da li je skup A neprazan. U slučaju da je skup A prazan, uvedene pretpostavke će biti protivrečne, ali legitimne. Definicija teoreme je da je to formula koja ima dokaz. Iskaz "ona teorema nema dokaz" je oksimoron. Možda to nije teorema (jer su se autori zeznuli), možda se dokaz zbog jednostavnosti prepušta čitaocu, a možda je izostavljen zbog složenosti, a ima ga u nekoj drugoj literaturi. Šta fali navedenom redosledu kdo Mateljevića? [ BrutalCoin @ 21.04.2023. 22:35 ] @
U tom tvom obrazloženju izostavio si "proizvoljna".
I zaista da piše "... neprekidna funkcija i Psi njena primitivna funkcija..." sve bi bilo matematički jasno. No, pošto si i ti (kao i ja što mislim da treba) izostavio "proizvoljna" onda smo to razrešili. Redosled kod Mateljevića i redosled koji si ti predložio nisu saglasni. Ti prvo definišeš ugao pa tek potom trigonometrijske funkcije a kod Mateljevića je obratno. Meni ne smeta, može i definicije preko stepenog reda, ali ne znam za druge. [ Nedeljko @ 21.04.2023. 23:49 ] @
"Proizvoljno x tako da..." znači "za x takvo da važe navedeni uslovi bez dodatnih pretpostavki". Sa ili bez reči "proizvoljno" značenje se ne menja.
Kompleksna analiza se uči nakon savladavanja geometrije i realne konačnodimenzione analize. Broj Pi nije morao ni da definiše, a što se ugla tiče, ne bavi se on geometrijom, nego kompleksnom analizom, tako da on pretpostavlja znanje geometrije i samo je tumači u kompleksnoj ravni. [ BrutalCoin @ 22.04.2023. 05:28 ] @
Nemoj zamenjivati teze uvodjenjem novih pojmova.
I opet odvajaš "proizvoljno" od konkretnog primera koji sam naveo. Pusti to. Citat: Kompleksna analiza se uči nakon savladavanja geometrije i realne konačnodimenzione analize. Broj Pi nije morao ni da definiše, a što se ugla tiče, ne bavi se on geometrijom, nego kompleksnom analizom, tako da on pretpostavlja znanje geometrije i samo je tumači u kompleksnoj ravni. Ako hoćeš da kažeš da iz toga sledi proizvoljna metodika nastave onda metodike nastave i nema. [ Nedeljko @ 22.04.2023. 13:33 ] @
Dobio si odgovor, ali bi da se prepucavaš.
1. Izbacivanjem reči "proizvoljna" u navedenom citatu se ne menja značenje. Objašnjeno je šta je značenje. 2. Niko nije rekao da je metodika nastave proizvoljna. Ona je proizvoljna do na poštovanje nekih principa. To što nije jednoznačno određena ne znači da je proizvoljna. Ne vidim problem u Mateljevićevoj kompleksnoj analizi u vezi pomenutog redoslaeda defincinija. [ miki069 @ 22.04.2023. 14:37 ] @
Jel može da se dokaže x<tg(x) a da se ne koristi limes koji dokazujemo?
[ BrutalCoin @ 22.04.2023. 16:40 ] @
Citat: Nedeljko Dobio si odgovor Kakav odgovor kad ništa nisam ni pitao. Na primer sin(x) je primitivna funkcija funkcije cos(x). I tu ništa nije proizvoljno. Proizvoljna je konstanta koja se može dodati na sin(x) i opet važi sin(x)+konstanta je primitivna funkcija funkcije cos(x). Citat: Nedeljko Ne vidim problem u Mateljevićevoj kompleksnoj analizi u vezi pomenutog redoslaeda defincinija. Naravno da kod Mateljevića ne postoji problem. Uostalom, već sam napisao da meni ne smeta. Mateljević je napisao knjigu iz koje čak i ja razumem definicije sinusa i kosinusa. Hoću da kažem da je prihvatljiv redosled izlaganja kod Matijevića iako je (za razliku tvog predloga) prvo definisao trigonometrijske funkcije pa tek potom ugao. [ BrutalCoin @ 23.04.2023. 07:42 ] @
Da se ispravim: u prethodnom tekstu umesto "izlaganja kod Matijevića" treba da piše "izlaganja kod Mateljevića" pa da nastavimo dalje.
U odgovoru članu @zzzz navodi se: Citat: Nedeljko: Procena ti je vrlo loša, a što se literature tiče: A) Tačke 1-7 - "Geometrija" Zorana Lučića. B) Tačke 8-9 su trivijalne na osnovu prethodnog. C) Tačke 11, 13-16 - Matematička analiza I Milosava Marijanovića. Pretpostavljam da se misli na knjigu "Euklidska i hiperbolička geometrija" Zorana Lučića. Dakle po predlogu člana @Nedeljko prvo ide geometrija a tek potom Matematička analiza. Medjutim uvidom u raspord časova Matemetičkog fakulteta očigledno je da student prvo prolazi ispit (matematičku) Analizu 1 (dva semestra uf) na prvoj godini a tek potom na drugoj godini studija predmet Osnovi geometrije gde se kao literatura navodi "1. Z. Lučić, Euklidska i hiperbolička geometrija, Beograd 1997.". Opet obratno od onog što predlaže član @Nedeljko studenti MF prvo obradjuju (Analiza 1) izvod i integral (pa i pojam primitivne funkcije sve sa limesom sin(x)/x, x-->0) a tek potom Osnove geometrije. Da ne bude imputacija, meni je prihvatljiv redosled koji je na matematičkom fakuletu i pozdravljam. Sad da se vratimo na Tačke 1-7: Citat: Nedeljko: 1. Definisati izometrije ravni i klasifikovati ih. 2. Definisati ugao kao geometrijski pojam (dve poluprave sa zajedničkim temenom dele ravan na dve oblasti itd.), kao i pojam pravog ugla. U Lučićevoj knjizi je obrnuto: Prvo u poglavlju GEOMETRIJA PORETKA uvodi definicije 5.Ugao i diedar (str. 28) a tek potom u sledećem poglavlju PODUDARNOST 10. ... Izometrije... (str. 79) definiše izometriju ravni. Opet, da ne bude imputacija, izlaganje kod Lučića je logično jer prvo uvedete objekte pa tek potom relacije nad tim objektima. [ miki069 @ 23.04.2023. 18:23 ] @
To je OK.
Ali nikakve veze nema sa dokazom limesa koji je tema i koji je neispravno izveden jer koristi samog sebe. [ BrutalCoin @ 24.04.2023. 07:09 ] @
Onda da se vratimo temi...
Citat: miki069 Jel može da se dokaže x<tg(x) a da se ne koristi limes koji dokazujemo? Možda razvojem u red? x + x^3/3 + 2x^5/15 + ... > x za x iz (0,Pi/2). [ miki069 @ 24.04.2023. 18:07 ] @
Razvoj u red koristi izvod od sin(x).
Taj izvod se ne može dokazati bez limesa koji dokazujemo. [ BrutalCoin @ 24.04.2023. 23:05 ] @
Funkcija sinus je rastuća na (0, Pi/2), ima inverznu arcsin koju izračunamo preko integrala za dužinu luka.
Onda arcsin'(x) = 1/Sqrt(1-x^2) pa po teoremi o izvodu inverzne funcije sledi sin'(x) = cos(x). [ BrutalCoin @ 25.04.2023. 09:54 ] @
Tj. sin'(fi) = cos(fi) da ne bude miksovanja argumanata sa arcsin.
[ miki069 @ 25.04.2023. 20:09 ] @
Integral koji daje arcsin(x) je posledica izvoda od arcsin(x).
Taj izvod se dokazuje korišćenjem činjenice da je izvod od sin(x) = cos(x) i teoreme o izvodu inverzne funkcije. Dakle ništa bez limesa. Jedno rešenje je da se dokaže nejednakost x < tg(x) bez korišćenja površine kruga. Ne znam da dokažem. Drugi put je da se površina kruga izvede kao limes Rimanove integralne sume. Ne znam da izvedem. Ako su ova dva puta nemoguća, treći bi bio skroz drugačiji način dokazivanja limesa sin(x)/x. Imam rešenje preko zbira dužina upisanih tetiva u kružni luk. Taj niz zbirova je rastući i odozgo ograničen sa x. Znači da je konvergentan. Ali nema garancije da konvergira ka x. Iako je intuitivno jasno da konvergira ka x. [Ovu poruku je menjao miki069 dana 25.04.2023. u 21:25 GMT+1] [ Nedeljko @ 26.04.2023. 02:07 ] @
BrutalCoin nastupa kao da postoji samo jedan ispravan redosled izlaganja.
Problem je što se trigonometrija tipično izlaže tako da se analiza i geometrija ne povežu logički utemeljeno. Može se dokazati da je u desnoj poluokolini nule sinus konkavna, a tangens konveksna funkcija. Odatle sledi da je funkcija 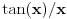 rastuća, a rastuća, a 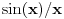 opadajuća, pri čemu važi nejednakost opadajuća, pri čemu važi nejednakost 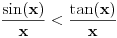 . Odatle se izvodi da traženi limes postoji i da je pozitivan i konačan. Pritom se "može napraviti izbor mernih jedinica" takav da taj limes bude jednak 1. . Odatle se izvodi da traženi limes postoji i da je pozitivan i konačan. Pritom se "može napraviti izbor mernih jedinica" takav da taj limes bude jednak 1.[ BrutalCoin @ 26.04.2023. 09:55 ] @
Citat: Nedeljko BrutalCoin nastupa kao da postoji samo jedan ispravan redosled izlaganja. Nemoj preterivati. Nisam ja osporio tvoj sistem nego postavljam pitanje kako to uklopiti u postojeći (tj. već uobičajeni) sistem. A postojeći sistem je kako sam napisao "ad-hok" tj. na osnovu iskustva. A problem x < tg(x) se u praktično celokupnoj literaturi zasniva no onome što su napisli Adnadjević/Kadelburg i oni pre njih. Tj. dokazuje se geometrijski preko površine kružnog isečka. Nakon dokaza x < tg(x) Adnadjević/Kadelburg dokazuju (na osnovu "dokazanog") da je lim(sinx/x)=1, x-->0. Zatim navode teoremu o izvodu inverzne funkcije i daju (arcsinx)' = 1/Sqrt(1-x^2) pozivajući se na tu teoremu. E sad je problem lim(sinx/x), x-->0 mada se u pomenutoj teoremi traži lim((f(x)-f(x0))/(x-x0)), x-->x0. A to nije lim(sinx/x), x-->0. Na primer, Ljaško/Boračuk samo daju lim(sinx/x)=1, X-->0, ali dokaz (trivijalno U knjizi za elekttrotehnički Mihajlović/Janić takodje koriste geometriju: Na krugu poluprečnika OA=OB=R sa centralnim uglom AOB=x zaključuju da važi: area trougla OAB < area sektora OAB < area trougla OAC area trougla OAB = R^2*sinx/2 area sektora OAB = luk AB*R/2 = R*x*R/2 = R^2x/2 area trougla OAC = OA * OC/2 = R*R*tgx/2 = R^2*tgx/2 Pa dobijaju R^2*sinx/2 < R^2x/2 < R^2*tgx/2 tj. sinx < x < tgx ■ Problem, x < tgx, se može rešavati i preko kompleksnih brojeva. Ali onda za kompleksan broj z = x + iy neko može da kaže da je to u stvari z = r(cosß + isinß), r = |z| i da sve ospori jer se javlja sinus. Citat: Nedeljko: Može se dokazati da je u desnoj poluokolini nule sinus konkavna, a tangens konveksna funkcija. Kako dokazuješ da je konveksna? Preko izvoda ili parametarskim putem? [ Bradzorf012 @ 26.04.2023. 19:04 ] @
Ljaško Bojarčuk.
Zaboravi izvode. [ Nedeljko @ 27.04.2023. 15:21 ] @
Citat: BrutalCoin: Citat: Nedeljko: Može se dokazati da je u desnoj poluokolini nule sinus konkavna, a tangens konveksna funkcija. Kako dokazuješ da je konveksna? Preko izvoda ili parametarskim putem? Prvo se dokazuje da je J-konkavna na intervalu 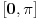 , odnosno da važi. , odnosno da važi.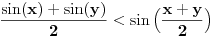 za za 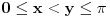 . .Za J-konkavnu funkciju se dokazuje da zadovoljava uslov 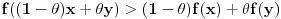 za za 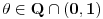 . .Takođe se dokazuje da je konkavna ako je lokalno ograničena ili neprekidna. Sinus je ograničen. [ BrutalCoin @ 27.04.2023. 17:41 ] @
To su definicije a ne dokaz.
U svim tim teoremama po literaturi, po pravilu se pretpostavi diferencijabilnost i koristi izvod da se dokaže konveksnost. No, nije bitno, uzmi da nisam ništa pitao. Jedna ideja je da se posmatraju tetive koje spajaju grafik funkcije i ako su tetive iznad grafika onda je funkcija konveksna. Može se teoretski dokazati a računarski realizovati i meni dovoljno. Citat: miki069 Razvoj u red koristi izvod od sin(x). U medjuvremenu sam malo računao. Ako uzmem izvod tg'(x) =1/cos^2(x) pa drugi izvod tg''(x) =2sin(x)/cos^3(x) Tu nigde ne vidim sin(x)/x a kako izgleda ni u sledećim izvodima se neće pojaviti. Zašto je onda problem da se preko razvoja u red pokaže x + x^3/3 + 2x^5/15 + ... > x za x iz (0,Pi/2)? [ miki069 @ 27.04.2023. 19:18 ] @
Izvod od tg(x) se ne može dokazati bez izvoda od sin(x).
Izvod od sin(x) se ne može dokazati bez limesa koji dokazujemo. [ BrutalCoin @ 27.04.2023. 22:16 ] @
Da, kad se ispiše po definiciji onda upravo tako "zaglavi".
[ Nedeljko @ 28.04.2023. 00:16 ] @
Citat: BrutalCoin: To su definicije a ne dokaz. Napisao sam šta treba da dokažeš. Dokaz J-konkavnosti sinusa se izvodi pomoću adicionih formula. Potrudi se malo. [ BrutalCoin @ 28.04.2023. 05:41 ] @
Ne treba ja ništa da dokazujem a tebi šta treba dokazuj sam.
[ Nedeljko @ 28.04.2023. 14:50 ] @
Ne treba meni ništa, samo onda ne razumem tvoj komentar koji sam citirao.
[ miki069 @ 29.04.2023. 00:39 ] @
Nije problem da se dokaže da je sin(x) "Dži konkavna", a tg(x) "Dži konveksna".
Ne vidim kako se posle toga dokazuje limes koji je tema? To što je tg(x)/x rastuća funkcija ne povlači da je x<tg(x). Mislim da bez dokaza te nejednakosti samo presipamo šuplje u prazno. [ Nedeljko @ 29.04.2023. 20:00 ] @
Iz J-konveksnosti i monotonije sledi konveksnost. Odatle sledi da je sinus konkavan, a tangens konveksan u desnoj poluokolini nule. Odatle sledi da za
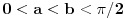 važi važi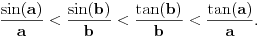 Odatle sledi da kada se  približava sa desne strane nuli, vrednost približava sa desne strane nuli, vrednost 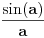 je pozitivna, raste i ograničena odozgo sa je pozitivna, raste i ograničena odozgo sa 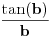 , pa ima konačan i pozitivan limes koji nije veći od , pa ima konačan i pozitivan limes koji nije veći od 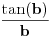 . Analogni iskaz važi i za tangens. Pošto je količnik sinusa i tangensa jednak kosinusu, koji je neprekidan i u nuli jednak jedinici, ta dva limesa su jednaka, konačna i pozitivna. . Analogni iskaz važi i za tangens. Pošto je količnik sinusa i tangensa jednak kosinusu, koji je neprekidan i u nuli jednak jedinici, ta dva limesa su jednaka, konačna i pozitivna.Koliki je taj limes, to zavisi od izbora mere ugla, koja je određena do na multiplikativnu konstantu, a koja se može odabrati tako da taj limes bude jednak jedinici. [ BrutalCoin @ 29.04.2023. 23:36 ] @
Za a = 0.1 i b = 1.5 je
sin(a) = 0.09983341664 sin(b) = 0.9974949866 Tada je sin(a)/a = 0.99833416646 sin(b)/b = 0.66499665773 pa je sin(a)/a > sin(b)/b [ miki069 @ 30.04.2023. 08:28 ] @
Tako i treba da bude jer je sin(x)/x opadajuća funkcija na intervalu (0, π/2).
U prvoj poruci je Nedeljko tako i napisao. U drugoj je okrenuo u rastuću. [ miki069 @ 30.04.2023. 20:28 ] @
Dokazao sam konkavnost za sin(x) na intervalu (0, π).
Kako ona povlači da sin(x)/x opada? [ miki069 @ 01.05.2023. 15:28 ] @
Ako prihvatimo da sin(x)/x opada, a tg(x)/x raste, poredak bi bio:
sin(b)/b < sin(a)/a < tg(a)/a < tg(b). [ BrutalCoin @ 01.05.2023. 16:50 ] @
Taj niz nejednakosti se može izvesti iz primera koji sam dao jer
tg(a)/a = 1.003346721 tg(b)/b = 9.400946631 I sad ako posmatramo limese lim ( sin(a)/a ) < lim ( tg(a)/a ) Ali lim ( tg(a)/a, a-->0 ) = 1 a u prethodnoj nejednakosti imamo znak manje, što bi povlačilo netačan zaključak lim ( sin(a)/a, a-->0 ) < 1 ! [ Nedeljko @ 01.05.2023. 19:38 ] @
[ BrutalCoin @ 01.05.2023. 21:07 ] @
Nedljko teško te je pratiti.
Napisao si onu nejednakost koja je pod znakom pitanja a nisi prokomentarisao šta si hteo da napišeš. Ako ostaje da si baš to hteo da napišeš onda može kako hoćeš. Dalje, ako je na primer lim( b(x) ) gornje ograničenje za a(x) onda je lim( a(x) ) = lim ( b(x) ). Jel dokazano (u prethodno napisanom) da je lim ( tg(x)/x, x-->0 ) gornje ograničenje za sin(x)/x ? Pitam zato što ne ispravljaš tipografske greške i ono što si napisao sa obrnutom nejednakošću nije baš dokaz. [ miki069 @ 01.05.2023. 23:10 ] @
Ako konveksnoj funkciji f(x) dokazujemo da f(x)/x raste, ciljna nejednakost bi trebala biti:
f(c-a)/(c-a) < f(b-a)/(b-a). Dokazano je nešta drugo. [ miki069 @ 02.05.2023. 06:30 ] @
Nizom ekvivalencija je dokazano:
(f(c)-f(a))/(c-a) < (f(b)-f(a))/(b-a) To ne znači da je f(x)/x rastuća funkcija. [ miki069 @ 02.05.2023. 08:45 ] @
Za a=0 i ako je f(0)=0, znači da je rastuća.
Za neko drugo a ne znači ništa. Ako f(0) nije nula, takođe ne znači ništa. Pošto je tg(0)=0, može se primeniti. Kada smo dokazali da traženi limes postoji, kako dokazujemo da je = 1? [Ovu poruku je menjao miki069 dana 02.05.2023. u 09:56 GMT+1] [ Nedeljko @ 02.05.2023. 17:14 ] @
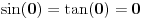 , pa iz konkavnosti funkcije , pa iz konkavnosti funkcije 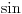 i konveksnosti funkcije i konveksnosti funkcije 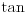 sledi da je sledi da je 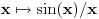 opadajuća, a opadajuća, a 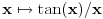 rastuća funkcija. rastuća funkcija.Monotone funkcije imaju limes u nuli sa desne strane. Pokazao sam kako se izvodi da je taj limes pozitivan i konačan. Ako uglove meriš u stepenima, a ne u radijanima, onda taj limes nije jednak 1. Međutim, moguć je izbor funkcije mere ugla (koja je određena jednoznačno do na multiplikativnu konstantu), tako da taj limes bude jednak jedinici. Za takav izbor funkcije mere ugla važi da je 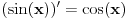 i i 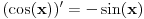 , pa je brzina tačke , pa je brzina tačke 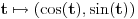 konstantno jednaka jedinici, odakle sledi da je ta funkcija mere ugla jednaka meri ugla u radijanima. konstantno jednaka jedinici, odakle sledi da je ta funkcija mere ugla jednaka meri ugla u radijanima.Edit: 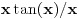 promenjeno u promenjeno u 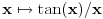 . .[Ovu poruku je menjao Nedeljko dana 02.05.2023. u 21:36 GMT+1] [ BrutalCoin @ 03.05.2023. 05:07 ] @
Svi prethodni navedeni metodi dokazivanja "padaju u vodu" jer se pozivaju na izvod sin' = cos.
Ti sad napišeš da važi (sin(x))' = cos(x) Šta je onda u tvom izvodjenju dokaza novo kad smo i za (sada već klasičan) geometrijski metod polazili od te iste pretpostavke ((sin(x))' = cos(x)) a zatim taj metod dokazivanja odbacivali upravo zbog te (nedokazane) pretpostavke? [ miki069 @ 03.05.2023. 08:13 ] @
Ne poziva se nigde u dokazu na izvod.
Kada prihvatimo da je limes = 1, dokazuje da je mera ugla bila u radijanima a ne u stepenima ili gradijanima. Koristi vektor brzine, da bi dokazao radijane. A brzina je prvi izvod radijus vektora. Za mene je dokaz korektan. Još samo da dokažem konveksnost za tg(x). Nije baš trivijalno kao dokaz konkavnosti za sin(x), ali je rešivo. [ BrutalCoin @ 03.05.2023. 09:13 ] @
Citat: Za takav izbor funkcije mere ugla važi da je (sin(x))' = cos(x) i (cos(x))' = -sin(x), pa je brzina tačke konstantno jednaka jedinici Prvo ima izvod "pa" na osnovu toga zaključuje da je brzina konstantno jednaka jedinici. Zar to nije korišćenje izvoda? Mislim, ono, nismo ni morali da potežemo Jensenove nejednakosti nago odmah, du - "imamo takvu meru ugla za koju je brzina konstanto jednaka jedinici!" Onda samo još da odgonetnemo kako smo izabrali baš takvu funkciju? Trial & error? [ miki069 @ 03.05.2023. 10:00 ] @
Kada bi ugao x merili u stepenima, onda bi rezultat limesa bio pi/180, a ne 1.
Kada bi ugao x merili u gradijanima, onda bi rezultat limesa bio neki treći broj. Ne znam koji, jer ne znam definiciju gradijana. Nedeljko je dokazao da je rezultat limesa konstanta veća od 0 i manja od beskonačnosti. Ako prihvatimo da je limes 1, onda tražimo meru ugla. Može i obrnuto. Mislim da je sve korektno. [ miki069 @ 03.05.2023. 13:32 ] @
Preko dužine upisanih tetiva.
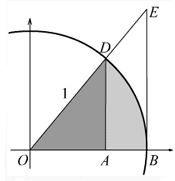 Preko kosinisne teoreme se lako dokaže da je dužina tetive BD jednaka 2*sin(x/2). Ako kružni luk podelimo simetralom ugla x, dobijemo dve upisane tetive čiji je zbir 4*sin(x/4). Posle sledeće podele uglova x/2 simetralama imamo 4 tetive čiji je zbir jednak 8*sin(x/8). Posle n-1 iteracije imamo da je zbir tetiva jednak 2^n*sin(x/(2^n)). Kada pustimo da n teži u beskonačno, intuitivno, zbir tetiva teži dužini kružnog luka x. To jest 2^n*sin(x/(2^n)) teži x. Odatle sin(x/(2^n)) teži ka x/(2^n), što je i dokaz traženog limesa. [ Nedeljko @ 03.05.2023. 14:17 ] @
[ miki069 @ 03.05.2023. 15:27 ] @
Da ne petljam sa simetralama.
BD = 2*sin(x/2) < x Da li može da se prihvati da kada x teži nuli da dužina tetive BD teži ka x? [ Nedeljko @ 03.05.2023. 19:56 ] @
Ne može jer je x promenljiva iz graničnog procesa. Verovatno si mislio da količnik te dve veličine teži jedinici. Opet, to zavisi od izbora funckije mere ugla.
Moguć je i pristup sa površinama, ali onda ima drugih stavova koje treba dokazati. [ BrutalCoin @ 04.05.2023. 10:48 ] @
Citat: miki069 Kada bi ugao x merili u stepenima, onda bi rezultat limesa bio pi/180, a ne 1. Sad sam ukapirao... Vi pod "funkcija mere ugla" podrazumevate jedinice mere. Ja to posmatram kao dva različita pojma. Onda u redu (za limes =1). Tada imaš odgovor i na pitanje Citat: Da li može da se prihvati da kada x teži nuli da dužina tetive BD teži ka x? Dužina tetiva nije funkcija mere ugla, jer ako bi dužinu tetiva uzeli za funkciju mere ugla tada za uglove α1 + α2 = α3 može biti M(α1) + M(α2) > M(α3) pa dužina tetiva nije odgovarajuća mera. [ miki069 @ 04.05.2023. 16:35 ] @
Nigde ne mogu da nađem stav da je obim pravilnog n-tougla veći od obima u njega upisane kružnice.
Dokaz tog stava bi ujedno bio i lagan dokaz ovog limesa. Dokazao sam konveksnost funkcije tg(x) na intervalu [0,π/2). [ Nedeljko @ 04.05.2023. 23:37 ] @
Za taj pristup preko površina treba dokazati da se mera ugla može definisati kao površina odgovarajućeg kružnog isečka jediničnog poluprečnika. To se dokazuje primenom invarijantnosti mere za izometrije i aditivnosti mere. Uvedena mera je polovina mere u radijanima. Onda se može primeniti metod sa površinama.
[ miki069 @ 22.05.2023. 08:39 ] @
[ Nedeljko @ 22.05.2023. 21:18 ] @
Prvo uvedi funkciju
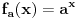 za za  i i  racionalno. Onda dokaži racionalno. Onda dokaži 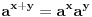 , , 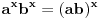 , , 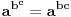 i monotoniju i iskoristi i monotoniju i iskoristi 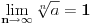 za za  da dokažeš da ako je da dokažeš da ako je 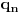 niz racionalnih brojeva koji teži nuli da je onda niz racionalnih brojeva koji teži nuli da je onda 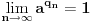 . To iskoristi da dokažeš sledeće: ako je . To iskoristi da dokažeš sledeće: ako je 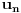 rastući niz racionalnih brojeva, a rastući niz racionalnih brojeva, a 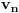 opadajući niz racionalnih brojeva, pri čemu je opadajući niz racionalnih brojeva, pri čemu je 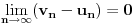 , onda mora biti , onda mora biti 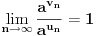 , odnosno , odnosno  . To ti omogućava da definišeš jednoznačno . To ti omogućava da definišeš jednoznačno 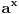 za za  i i  realno kao jedinstevno neprekidno produženje sa racionalnih eksponenata na realne. realno kao jedinstevno neprekidno produženje sa racionalnih eksponenata na realne.Funkcija 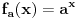 je za je za 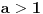 J-konveksna i neprekidna, pa je konveksna, pa je funkcija J-konveksna i neprekidna, pa je konveksna, pa je funkcija 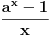 rastuća. Kada sa desne strane rastuća. Kada sa desne strane  teži nuli, onda teži nuli, onda 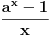 opada, ali je stalno veće od nule, pa konvergira nenegativnoj vrednosti. Za opada, ali je stalno veće od nule, pa konvergira nenegativnoj vrednosti. Za 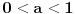 je je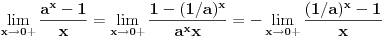 , ,pa se konvergencija svodi na konvergenciju u slučaju da je 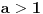 . Analogno važi i u slučaju kada . Analogno važi i u slučaju kada  teži nuli sa leve strane. Pošto smo dokazali konvergenciju, možemo definisati funkciju teži nuli sa leve strane. Pošto smo dokazali konvergenciju, možemo definisati funkciju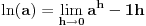 . .Sada se lako izvodi da je 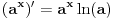 . .Ako je 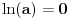 , onda je , onda je 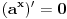 pa je funkcija konstantna i jednaka vrednosti pa je funkcija konstantna i jednaka vrednosti 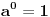 pa je pa je 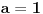 . Dakle, za . Dakle, za 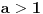 je je 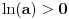 , dok za , dok za 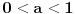 važi važi 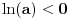 . Iz identiteta . Iz identiteta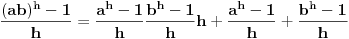 sledi da je 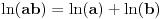 . .Odatle sledi da je 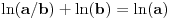 , odnosno , odnosno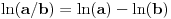 , ,  . .Takođe, smenom 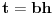 se dobija da važi se dobija da važi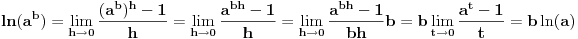 . .Sada je lako izvesti strogu monotoniju funkcije 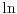 . Za . Za 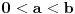 je je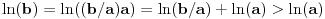 . .Slično, iz 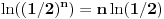 i i 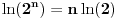 sledi neograničenost funkcije sledi neograničenost funkcije 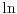 i odozgo i odozdo. Dokažimo neprekidnost. i odozgo i odozdo. Dokažimo neprekidnost.Iz monotonije sledi da postoje limesi i sa leve i sa desne strane. Svaka monotona funkcija može imati najviše prebrojivo mnogo tačaka prekida, pa postoje tačke u kojima je funkcija 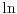 neprekidna. Neka je neprkidna u tački neprekidna. Neka je neprkidna u tački  . Za svaki niz . Za svaki niz  koji konvergira nekoj tački koji konvergira nekoj tački 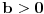 važi da niz važi da niz 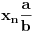 konvergira ka konvergira ka  , pa važi , pa važi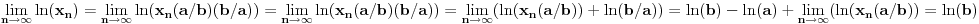 , ,pa je neprekidna i u tački  . Dakle, neprekidna je svuda. Pritom je . Dakle, neprekidna je svuda. Pritom je 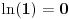 i sa ob strane neograničena i strogo rastuća, pa je bijekcija skup i sa ob strane neograničena i strogo rastuća, pa je bijekcija skup 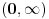 na na  , pa postoji jedinstvena vrednost , pa postoji jedinstvena vrednost  za koju je za koju je 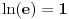 . Tada važi . Tada važi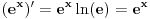 , ,a samim tim i 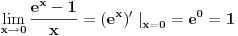 . .Pritom je 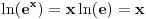 , ,pa je 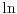 ništa drugo do inverzna funkcija funkcije ništa drugo do inverzna funkcija funkcije 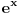 , odnosno logaritam za osnovu , odnosno logaritam za osnovu  . Izvod funkcije . Izvod funkcije 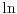 se sada može izvesti kao izvod inverza funkcije se sada može izvesti kao izvod inverza funkcije 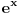 . .[ sikira069 @ 18.02.2024. 21:38 ] @
Citat: miki069: Preko dužine upisanih tetiva.  Preko kosinisne teoreme se lako dokaže da je dužina tetive BD jednaka 2*sin(x/2). Ako kružni luk podelimo simetralom ugla x, dobijemo dve upisane tetive čiji je zbir 4*sin(x/4). Posle sledeće podele uglova x/2 simetralama imamo 4 tetive čiji je zbir jednak 8*sin(x/8). Posle n-1 iteracije imamo da je zbir tetiva jednak 2^n*sin(x/(2^n)). Kada pustimo da n teži u beskonačno, intuitivno, zbir tetiva teži dužini kružnog luka x. To jest 2^n*sin(x/(2^n)) teži x. Odatle sin(x/(2^n)) teži ka x/(2^n), što je i dokaz traženog limesa. Ako pustimo da n teži u beskonačnost imamo dokaz traženog limesa. Korektno? Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|