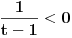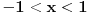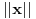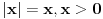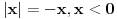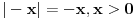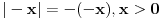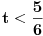posebno razmatraj intervale koje razgraničavaju tačke -1, -2/3, 0, 2/3, 1

@Nepoznat covek

Preporucio bih da naucis bar Latex komandu za razlomke, radi bolje citljivosti. Dakle, naredba je \frac{}{}, prva zagrada brojilac, druga imenilac. Na primer kod [ tex]\frac{a}{b}[/tex ] daje 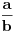. Imas i drugu varijantu (koja se meni manje svidja) [ tex]a \over b [/tex ] ([ tex] tagovi su malo siri, jer bi se inace konvertovalo u Latex kod).

Inace, najprirodnije je prvo nejednacinu svesti na dva slucaja u zavisnosti od 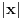, a posle resavati svaki slucaj posebno (pazeci gde se krece ).

Možeš riješiti zadatak i tako da uvedeš smjenu |x|=t. Nejednačina se svede na sljedeći oblik: tj. tj. . Rješenje polazne nejednačine je: .

@Sini82

Nije ti dobro resenje (proverio sam Wolframom), stavi na primer i dobices da je leva strana jednaka 4.

Jednacina nema resenja za pozitivan imenilac

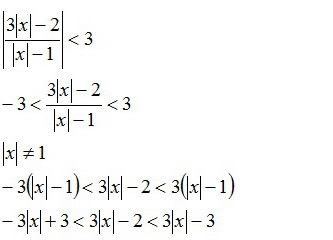Nadam se da uvidjate zbog cega.

Za negativan imenilac imamo resenje.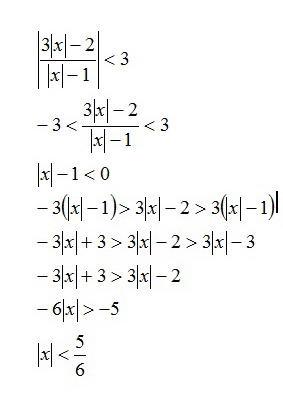

Opravio sam ga :)

_{[Ovu poruku je menjao bobanex dana 18.06.2012. u 00:27 GMT+1]}

Ma kako nema. Ubaci na primer i leva strana ce biti jednaka 1, sto zadovoljava nejednacinu.

I dalje mislim da je najbezbolniji onaj moj način razdvajanja na intervale. U ovom gornjem razmatranju bobanexa, zanemareno je da množenje nejednačine pozitivnim i negativnim vrednostima mora da se razdvoji.
Radeći sa intervalima dolazim do rešenja, nadam se da nisam pogrešila, (-5/6, 5/6)


_{[Ovu poruku je menjao berazorica dana 18.06.2012. u 01:27 GMT+1]}

Samo izbegavaj uglaste zagrade ne znam otkud ti :)

To ti kazem krajevi su visak u njima je izraz jednak 3, a treba da bude manji od 3 a ne manji ili jednak.

Da nas zbuni, za sta bi drugo.

Da, da, u pravu si.

Leleeeee, odo' ja lepo da kopam kanale k'o čovek Šalim se, skontao sam, nego ima mnogo da se pazi na uslove.. još jedno pitanjce.. Koliko je apsolutna vrednost od apslolutne vrednosti x?

Hajde, razmisli, pa napiši šta misliš, pa ćemo da proverimo i ispravimo ako to nije to.

Hajd' da napišem moje mišljenje.. :)
Dakle:
Ako nije bitan redosled rešavanja apsolutne vrednosti, onda ću ja prvo unutrašnje da rešim.

To liči otprilike ovako i

Dakle, onda pod ovom drugom apsolutnom vrednošću imamo dva slučaja: i

I sad i , i

Iskomplikovao si ga, ali kad si vec kreno tako, u ove dve poslednje varijante treba da pise -x>0 i -x<0. Pa se to malo sazme posle.

Pa to, ali sam množio sa -1 da bi se izgubio ''-'' kod x.. Da li je dozvoljeno ovo primenjivati?

Ako si vec mnozio sa -1, mislim da si to lose uradio. Mogao si da zakljucis vec ranije da je |-x| = |x|.

Rješavao sam zadatak, samo bez vanjskih zagrada apsolutne vrijednosti, zamijenio sam ih običnim. Nije ovaj zadani ali tačno sam ga riješio.

Može na isti način da se riješi i zadani zadatak:

. Desnu nejednakost smo riješili, ostaje nam da riješimo lijevu i nađemo presjek njihovih skupova rješenja.

Rješenje lijeve nejednakosti je ili . Uzimajuci u obzir i rješenje desne nejednakosti , kao presjek njihovih skupova rješenja dobijamo: tj. . Pitajte Wolfram ako ne vjerujete ;-).

Ovo se verovatno odnosi na mene, al dobro.



Da, ali ti si rekao



Pa sam te zbog toga ispravio, nigde nisam video da je to resenje jednog dela zadatka.

Al sve u svemu, bitno da je resen zadatak na jos jedan nacin.

Haha! Hvala na ispravci, potpuno si bio u pravu kada si me ispravio! Jeste na tvoj račun ali nije zlonamjerno ;-). Simpatično mi je to sa Wolframom, zato sam se našalio, nemam naviku da pomoću njega provjeravam rješenja.

Sve je ovo lako...