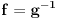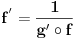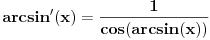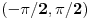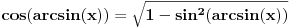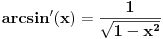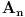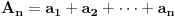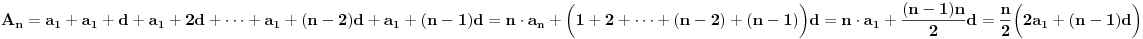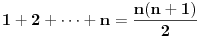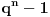[ Open93 @ 20.06.2012. 23:20 ] @
| Treba mi pomoc. Spremam prijemni iz matematike za fakultet, gradivo je prilicno obimno i veoma je tesko da popamtim sve formule. Pa sam ja dosao na izvanrednu ideju, da izvedem sve formule radi jednostavnosti ne bih da bubam samo za prijemni jer bih voleo da mi ostane nesto u glavi. ali to cu pre svega raditi iz oblasti gde ima pregrst formula kao npr. analiticka geometrija u ravni, trigonometrija, izvodi, stereometrija, planimetrija... A posto na samoj elektronici neophodna je dobra podloga matematike, pogotovo izvoda i integrala. Za sad interesuje me samo tablica osnovnih izvoda, znam da su svi oni izvedeni iz formule lim(dx->0)=(f(x+dx)-f(x))/dx. Ove pocetne nije problem trazenje izvoda konstante, ali se problem javlja kod arctan x ili arcsin x koji su slicni a tezi su za pamcenje. Interesuje me da li je ovo pametno raditi pred prijemni i da mi date jos neki savet, nisam tremaros (za sad), ne plasim se mnogo matematike jer i ako sam iz elektrotehnicke skole, "dovoljno" dobro vladam matematikom za srednju skolu ali svaki savet bi mi dobro dosao. Inace zelim da upisem E1 u Novom Sadu na FTN-u. Molio bih za pomoc znacilo bi mi puno, izvinite sto davim, unapred sam vam zahvalan... |