Mozda moze da se iskoristi .

Posto je , bice .

Ovaj poslednji izraz je jednak nuli za . Probaj da zavrsis.

Kad konstatuješ da polazni izraz treba da bude deljiv sa , onda posebno pokazuješ deljivost za svaki činilac, tako što u izrazu prvo zameniš sa i tako i za ostala dva, a deljivost sa tri dobijaš rastavaljanjem izraza po gornjem (darkosos) receptu.



_{[Ovu poruku je menjao berazorica dana 25.06.2012. u 12:15 GMT+1]}

hvala vam puno

ako imam da je ,

potrebno je pokazati da je deljivo sa 3,odnosno kad ovo rastavimo ,potrebno je pokazati da je deljivo sa 3,kako to mogu da dokazem?

jel moze ovako da se dokaze
isto uradimo i za b i za c,pa dobijemo,a kako je ,dobijamo da je deljivo.

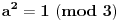
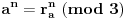
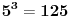
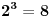
Uh, odakle ti da je ? Ja bih probao ovako: prvo, ako a ima ostatak r_a pri deljenju sa 3, onda je . Na primer, posto je 5 mod 3 = 2, je po modulu 3 isto sto i a to daje ostatak opet 2 pri deljenju sa 3. Uocavas sta se pritom desava? Pa smanjuje se broj, jer uzimas ostatak umesto celog broja, to je uvek manje. Kada imas vece stepene, mozes tako kao sti si sama postupno stepenovala, da dodjes brzo i lako do ostatka.

Posebno kada se radi o manjem broju po kojem se radi moduo, kao sto je ovde to 3, jer ostaci su samo 0, 1 i 2. Jasno je da ce prilikom stepenovanja 0 uvek biti 0, a 1 uvek biti 1. Dakle ostaje samo da se razmotri 2, tj. kako izgledaju mod 3 brojevi kada se 2 stepenuje?

Dobro je primetila da za brojeve (proveri, imaš samo dva moguća ostatka) koji nisu deljivi sa 3 važi , a samim tim i . No, ovo poslednje svakako važi i za brojeve deljive sa 3.

Znam, video sam vec, jer je 2²=4=1 (mod 3), na to sam i hteo da ukazem. Pa, moguce je da je ona to i radila, samo zaboravila da razmotri a = 0 (mod 3), makar za ovaj prvi korak...

E da, jos nesto @tikiliki86: nema potrebe da izraz sa 51. stepenom dalje rastavljas da bi dobila 17. stepen, jer istim rezonom dobijas da to vazi i za 51. stepen. U stvari, za svaki neparan.