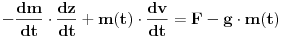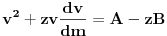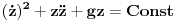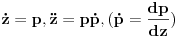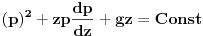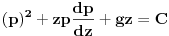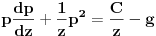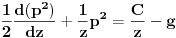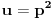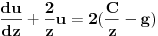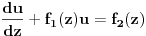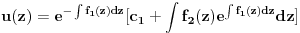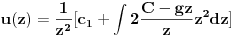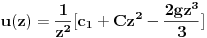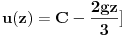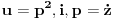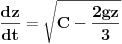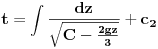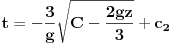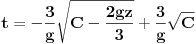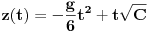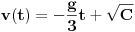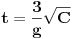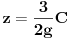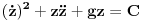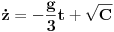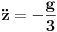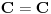[ donatela @ 28.06.2012. 15:25 ] @
| Imam problem da riješim diferencijalnu jednačinu i da dobijem zavisnost visine od vremena kretanja tijela vertikalno u vis,pod djelovanjem konstantne sile.JEDNAČINA JE-dz/dt*dz/dt+z(t)*dv/dt=F-g*z(t) dz/dt=v(t) tj brzina ,F=const. g*z-sila teže .Ovo je drugi njutnov zakon kretanja tijela promjenljive mase.Dobijem dif.jednačinu: v^2+z*v*dv/dz=A-B*z A,B su konstante.MOLIM ,DA LI MI NEKO MOŽE POMOĆI DA RIJEŠIM OVU JEDNAČINU I DA TO BUDE PARABOLA |