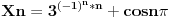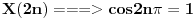Počni od , i dalje ćeš se lako raspetljati.

Hvala puno, mislim da sad trebam samo racionalisati ovaj izraz po sinusom, ako se ne varam...trenutno nemam papira kod sebe :D
A joooj, hvala puno, razmisljo sam o smjeni, i da transformišem izraz pod limesom, ali nisam se sjetio ideje da nesto treba DODATI :)

naci tacke nagomilavanja i donji limes niza ciji je opsti clan..... e sad ovako sam ja uradio... za a ovo pa onda ovo ide u beskonacno?? a za a ostalo pa ide -1 pa je to donji limes??... E sad da li je ovo dobro i koje su tacke nagomilavanja

Članovi sa parnim indeksom teže u +beskonačnost.
Članovi sa neparnim indeksom se nagomilavaju oko -1.
-1 je jedina tačka nagomilavanja. Da li je i tačka konvergencije niza?

znaci dobro je ono.... Ako je niz konvergentan, njegova granična vrijednost je ujedno i njegova jedina tačka gomilanja---po ovome bih ja rekao da jeste( mada nemam pojma :D )....

Upravo tako:
Ako je niz konvergentan, njegova granična vrednost je ujedno i njegova jedina tačka gomilanja.
Obrnuto ne mora da važi.
Ovo je lep primer da -1 jeste jedina tačka nagomilavanja, ali da nije tačka konvergencije.

Razlika je što u tome što u proizvoljnoj okolini tačke nagomilavanja, počevši od nekog člana niza, mora de se nađe beskonačno članova niza, ali ne i svi članovi niza.
Kod tačke konvergencije u njenoj proizvoljnoj okolini, počevši od nekog člana niza, mora de se nađu svi članovi niza, od tog člana pa do beskonačnosti.

Za okolinu od recimo 0.001, što daje interval od -1.001 do -0.999 ćeš obuhvatiti beskonačno članova niza.
Recimo (lupam napamet): 713-ti, 715-ti, 717-ti, ... i svi ostali članovi sa neparnim indeksom - njih beskonačno mnogo, ali ne i svi.
-1 jeste tačka nagomilavanja.
Ali u tom intervalu neće biti 714-tog, 716-og... člana i zato -1 nije tačka konvergencije.

_{[Ovu poruku je menjao miki069 dana 10.11.2012. u 01:42 GMT+1]}

U proširenom skupu realnih brojeva postoji još jedna tačka nagomilavanja - beskonačnost.

Da bi niz bio konvergentan u proširenom smislu (tj. u proširenom skupu realnih brojeva), potrebno je i dovoljno da u proširenom skupu realnih brojeva (gde uvek ima barem jednu tačku nagomilavanja) ima jednu jedinu tačku nagomilavanja. Da bi bio konvergentan u klasičnom smislu, ta tačka nagomilavanja treba da bude konačna. beskonačno i minus beskonačno nisu tačke nagomilavanja ako i samo ako je niz ograničen. Dakle, da bi niz u klasičnom smislu bio konvergentan potrebno je i dovoljno da bude ograničen (kada ima bar jednu tačku nagomilavanja) i ima tačno jednu tačku nagomilavanja.