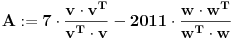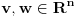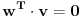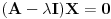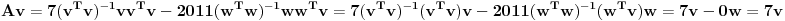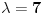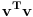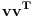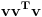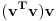Nesto mi tu cudno, ako su v i w vektori, onda ne postoje oba proizvoda, v sa v transponovano i obrnuto. To moze samo ako su to kvadratne matrice. Da nije nesto pogresno u postavci? A ako je v zaista vektor, v*v^T je broj...

kako ce V*V^T biti broj? pretpostavit' cemo da su to kvadratne matrice, onda rezultat treba da bude matrica (pa makar to bila matrica oblika [a], ali je to opet matrica, nije broj). Evo pogledao sam jos jednom tekst zadatka, i takav je kako sam ga ovdje napisao.

Pa, ti u samoj postavci deliš nulom.

Pa ako je v iz Rⁿ npr. v = (0,1,-3), koliko je v*v^T?

ako je v=(0,1,-3), onda je v*v^T=(0*0+1*1-3*(-3))=(10). matrica koja ima jedan jedini elemenat. nedeljko, pogledaj jos jednom uslov zadatka. ne dijeli se s nulom.

Hajde onda probaj da uradis sa tim primerom v^T*v...

Sad vidim šta sam loše video. OK,

.

Dakle, .

darkosos

Vektor mu je kolona, a ne vrsta, tako da je skalar, a kvadratna matrica čiji je red jednak dimenziji vektora.

Nedeljko, hvala ti mnogo. mi smo bili tako blizu rjesenju, i svo vrijeme se vrtili oko njega. trebalo je sve samo pomnoziti sa v :) jos jednom hvala.

Izgleda da sam nesto pozaboravljao, ono definitivno ne moze da se mnozi i ovako i onako kao sto bi se mnozile matrice, tj. kada se vektor posmatra kao matrica u kojoj je jedna dimenzija 1.

Nasao sam ne wp neki "direktan" proizvod, pise se bez ikakvog znaka, u kome se zaista dobija matrica n x n, ali tada ne moze da se koristi ista oznaka za proizvod. Ne secam se koji je domaci izraz za to, "dijadski"? Takodje, potvrdio sam da matrica 1x1 zaista jeste skalar, tj. broj. I takodje sam pretpostavio da treba da se mnozi sa v, nego nisam stigao zbog toga sto mi je ono izgledalo nelogicno... Lako je naravno biti general posle bitke :D

A šta smeta da se matrično pomnoži?

Proizvod matrice formata m x n i matrice formata n x p je matrica formata m x p. Dakle, proizvod matrice reda m x 1 i matrice formata 1 x m je matrica formata m x m, a proizvod matrice formata 1 x n i matrice formata n x 1 je matrica formata 1 x 1, koja se često identifikuje sa skalarom, mada u ovom zadatku to nije neophodno.

Svaka matrica se može množiti sa svojim transponatom.

Pozdrav opet :) ima li objasnjenje zasto se proizvod na -1 (inverzni nazivnik) mnozi s lijeva a ne s desna s brojnikom? Je li to bitno ovdje? Takodjer, kako si ti uspio dobiti iz ovaj clan , cudna komutativnost mnozenja matrica.

Za matrice i skalare važi zakon (aA)(bB)=(ab)(AB). Što se matrice formata 1 x 1 tiče, ona je jednaka svojoj jedinoj komponenti pomnoženoj jediničnom matricom formata 1 x 1.

Da, stvarno... Ne znam, zasto sam mislio da ne moze, valjda mi je smetala predstava da je leva horizontalna a desna vertikalna... A samo treba broj kolona leve da bude jednak broju vrsta desne... Moracu cesce da koristim olovku i papir :)