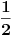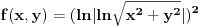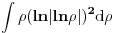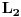[ malada @ 17.08.2012. 01:29 ] @
Molio bih za malu pomoc oko ovog integrala. Tj treba da izracunam dvostruki integral po krugu sa centrom u koordinatnom pocetku poluprecnika od funkcije
Presao sam na polarne koordinate i rijesio se jedne promjenljive, ali sad imam

E sad jedino da picim neke parcijalne integracije do besvijesti. Ako neko ima neku elegantniju ideju, neka javi.

Hvala unaprijed

[Ovu poruku je menjao malada dana 17.08.2012. u 02:43 GMT+1]
[ miki069 @ 17.08.2012. 13:16 ] @
Jesi siguran da si dobro prepisao zadatak?
Ovaj možeš da pičiš samo jedan korak parcijalnom integracijom, posle toga smena i dobija se nerešiv integral.
[ malada @ 17.08.2012. 16:57 ] @
Ma jesam, treba da pokazem da ova f-ja pripada prostoru nad ovim krugom, tj da pokazem da pripada , ali za izvode cu lako jer su integrali od izvoda nula.
[ malada @ 17.08.2012. 17:09 ] @
A koji se nerjesiv integral dobija? Mozda moze da se svede preko gama i beta funkcija, sto bi opet znacilo da je manji od beskonacno...
[ Nedeljko @ 17.08.2012. 17:31 ] @
Treba li da izračunaš integral ili da dokažeš da je konačan ili da ga oceniš? Kako glasi ceo zadatak?
[ darkosos @ 17.08.2012. 18:48 ] @
Po ovome sto je napisao rekao bih da samo treba da pokaze da je < 00, dakle dovoljno je da se proceni...
[ Nedeljko @ 17.08.2012. 21:01 ] @
Ako treba samo da dokaže da je ta funkcija u L2, onda se može pozvati na ograničenost podintegralne funkcije kod integrala u polarnom obliku.
[ malada @ 19.08.2012. 16:19 ] @
Hvala Nedeljko, nisam uopste uzimao u obzir da se mnozi sa "ro".