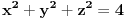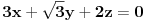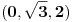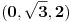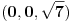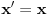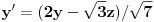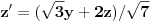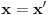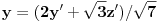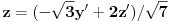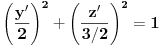Da eliminišeš x.

Dakle, izrazi x iz jednačine ravni, ubaci to u jednačinu sfere i čiča-miča i gotova priča.

Hvala puno. Znaci kad ovo ubacim samo jos treba da izvrsim rotaciju i onda dobijam jednacinu elipse

Ne, nikakvu rotaciju. Samo ubaci i dobio si jednačinu elipse (doduše neće imati kanonski oblik, ali je tačna).

Hm pa u zadatku traze kanonski oblik, ali to je zaista tesko naci, jer su brojevi nezgodni za racunanje.

E, ako tako piše, onda svedi.

Razmisli takođe o tome da se rotacija može odrediti pomoću vektora ravni koji preseca sferu.

Ako mozes samo malo detaljnije da objasnis to pomocu vektora ravni kako ide.Treba naci ugao sa yOz ravni?

Vidi šta je normalna projekcija tog vektora. Mala poluosa je paralelna njemu.

Normalna projekcija na yOz?
To bi bio vektor
I sad ako uzmem ugao koji taj vektor zaklapa sa y osom za ugao rotacije, ne izgubim zy clan jednacine krive, a to znaci da nisam uradio kako treba?

Suprotan ugao, tako da slika tog vektora legne ili na Oy osu ili na Oz osu.

Ovaj ugao?
Sa njim nisam uspeo...

Šta treba da uradiš sa vektorom da bi dobio na primer vektor ?

,
,
.

Šta je obrnuta transformacija?

,
,
.

Dobija se

.

Ako ste radili matricu kvadratne forme, radi preko nje.