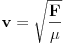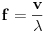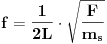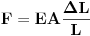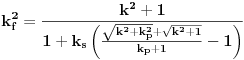|
|
[ darkosos @ 22.08.2012. 13:48 ] @
|
| Da li neko moze da napise koje formule bi opisivale sledecu situaciju, koja je vezana za sviranje gitare:
Dakle, zica je na gitari rastegnuta izmedju dve tacke i ima dva osnovna oslonca, izmedju kojih vibrira;
pritiskom zice na neki od pragova, smanjuje se deo zice koji vibrira i povecava se frekvenca.
Mene sada zanima sledeca situacija (zavijanje zice): dakle, pritiskam zicu o prag i povlacim je prstom u pravcu samog praga, tako da dobijem zeljeni ton (frekvencu);
Kako bi mogao da izracunam npr. koliki otklon treba da se napravi od polaznog pravca zice i kolikom silom treba da se deluje?
Jasno je da zica menja ton zato sto je sada zategnuta vecom silom, i mozda moze da se zanemare delovi zice koji se nalaze npr. od konjica do civije i od kobilice do mesta gde je pricvrscena na telu gitare.
Ne znam sta je sve potrebno od velicina, ali recimo da znamo duzinu zice, precnik zice, silu kojom je zategnuta i mesto na kome vrsimo zavijanje, npr rastojanje od konjica. Takodje, ako je potrebno, mozemo pretpostaviti da je zica celicna. |
[ darkosos @ 30.08.2012. 08:12 ] @
Pi bre, bas niko... Raspust? :)
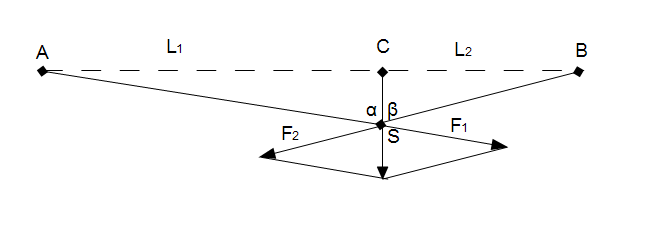
Evo neka slidza da pomogne... Recimo da je zica fiksirana za dve fiksne tacke A i B. I recimo da ako se "pridrzi" za C, daje frekvencu f. Ako zelim da dobijem frekvencu f1 zatezuci zicu u tacki C, tako da dodje u C 1, interesuje me kolikom silom treba da se deluje i koliki je otklon CC 1?
 [ Odin D. @ 30.08.2012. 21:47 ] @
[ darkosos @ 31.08.2012. 09:13 ] @
Na zalost, tamo nema primera za ono sto sam ja pitao...
[ djoka_l @ 31.08.2012. 09:43 ] @
Tamo nema primera zato što ono što ti trežiš nije trivijalno.
Brzina zvuka u žici je proporcionalna sili zatezanja žice, a obrnuto proporcionalna podužnoj masi. 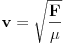
Sa druge strane, talasna dužina prvog harmonika je 
Frekvencija je u vezi sa brzinom i talasnom dužinom 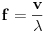
Dakle, povećanjem sile zatezanja, povećava se frekvencija.
Međutim, ti u tvom primeru nemaš prosto zatezanje (kao kada bi zavrtao čiviju), niti skraćivanje žice (kao kada pritisneš iza praga), već elastičnu deformaciju. Za to ti treba Jungov moduo materijala, i malo diferencijalnih jednačina.
Nažalost, tu ne mogu da ti pomognem, ali se nadam da sam ti ukazao na pravac istraživanja.
http://en.wikipedia.org/wiki/Elasticity_(physics)
http://en.wikipedia.org/wiki/Young%27s_modulus
http://en.wikipedia.org/wiki/Stress_(mechanics)
http://en.wikipedia.org/wiki/Deformation_(mechanics)
[ darkosos @ 31.08.2012. 09:51 ] @
Ok, hvala, ovo je vec mnogo korisnije :)
[ Odin D. @ 31.08.2012. 20:59 ] @
Citat: darkosos: Na zalost, tamo nema primera za ono sto sam ja pitao...
Tamo ima sve sto si pitao, samo na zalost, izgleda da ti to ne razumijes.
A ovo sto mislis da ti pomaze u tom titranju - bas ti nista nece biti od pomoci u tome sto te zanima. [ darkosos @ 31.08.2012. 21:50 ] @
Moguce je da ne razumem, pa eto zamolio bih te da mi objasnis. Uostalom, to i jeste razlog sto sam ovde postavio pitanje...
[ darkosos @ 31.08.2012. 22:19 ] @
Evo nekog mog pokusaja, cisto za sada koncepcijski, pa mozda neko pritekne sa necim konkretnim...
Dakle, ideja je da se sila zavijanja rastavi na komponente koje "drze" dva dela zice, kao na slici. E sad, da je to samo nova fiksna tacka, sve bi bilo lako, ali doslo je do izduzenja zice na oba dela, SA i SB.
Prvo pitanje je da li je uopste pritom C otislo u S? Ako jeste, mozda bi moglo ovako: izracunam kojom silom je AC izduzeno u AS i BC u BS; oduzmemo sile kojom deo zice BS "vuce" deo AS i obrnuto; to sto dobijem saberem i dobijem silu zavijanja.
Ima li ovo nekog smisla?
 [ ac1bd4 @ 31.08.2012. 23:22 ] @
Sve ti je djoka_l objasnio samo malo ćeš teško naći Jungov moduo elastičnosti za gitarske žice. No možeš ga izmeriti relativno lako ali ako sve to planiraš da koristiš samo da bi znao dokle da povučeš žicu kada treba da benduješ onda bi ti tu sluh više pomogao. U svakom slučaju možeš iskoristiti tjunere za gitaru (naročito na kompu) da ti izmeri frekvenciju.
[ zzzz @ 31.08.2012. 23:50 ] @
Kod transferzalnih oscilacija žice očigledno je da je poprečno pomjeranje mase
daleko intezivnije (veća amplituda) od podužnog.Zato se promjena zategnutosti žice pri izlasku iz osnovnog položaja opravdano zanemaruje.
Poprečna sila koja ubrzava masu nastaje zbog zakrivljenosti žice.Uzme se diferencijalno mala dužina žice i nađe ta poprečna sila pomoću prvog izvoda.
Ubrzanje je drugi izvod poprečnog kretanja po vremenu.Uz još neke idealizacije,Početni uslovi, uslov da po cijeloj dužini imamo istu frekvenciju,+malo truda može se napisati i rješiti diferencijalna jednačina. Osnovna frekvencija je približno:
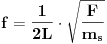
L je dužina žice,F sila zatezanja,a m_s je masa po jedinici dužine.Formula se dobro slaže sa eksperimentalnim mjerenjem.
Pritisak na prag gitare takođe ne mjenja značajno silu zatezanja,već samo L pa su u skladu sa tim napravljeni razmaci za željene frekvencije.
[ darkosos @ 01.09.2012. 11:13 ] @
@ac1bd4
Da, slazem se da bi sluh pomogao :) Ovo bi eventualno mogao da koristi robot koji svira, mada ako dovoljno brzo meri frekvencu, sa nekim mailm latency, znao bi kad da stane.
Ako neko od pristunih svira gitaru, a ja to radim vec 25 godina, zna da zavijanje zice tako da ima bas odredjeni ton nije ni fizicki lak posao (posebno ako se to radi za 2 ili vise polustepena), a nije lako ni proceniti koliko treba da zategnes. U principu, ako ides na sluh, to moze da prodje ako to radis polako i polako "ulazis" u potreban ton. Ako to treba brzo uraditi, onda sluh pomaze samo da saznas da li si dobro uradio :) Jer u principu, ako preteras, efekat je poprilicno ruzan, dok kad "podbacis" nije toliko strasno, ali iskusno uvo cuje da li je svirac namerno promasio ili se zahebo (moje iskustvo kao i slusanje mnogo gitarske muzike mi govori da je jako malo gitarista koji ovo rade na pravi nacin - uz napomenu da nije uvek potreba da se pogodi neki ton od 12 - i mnogo razlicitih tonova van onih standardnih moze zvucati veoma dobro).
Sve u svemu, ovo najvise postaje pitanje osecaja, koji se moze izgraditi samo kroz dugotrajnu vezbu. S' obzirom da mi je to hobi, zeleo sam da malo potpomognem svojim prsitma nekom intuicijom o tome kolika mi sila treba ili koliki otklon. Najvise zato da bih mogao da uporedim ono sto se desava na jednoj zici, na razlicitim mestima na vratu, kao i sa razlicitim zicama. Uostalom, sve ovo je vise radoznalost, nisam znao da ovo moze da bude tako komplikovano, cak i ako izostavim, kako je i zzzz rekao, trenje izmedju zice i praga, to sto prst nije jedna tacka, to sto ja prstom pritom ne guram samo zicu, itd...
@zzzz, ako napises tu DJ, obecavam da cu probati da resim, ili postovati to na forumu matematika :D
Niko nije komentarisao moj pokusaj, znaci da ne valja?
[ djoka_l @ 01.09.2012. 11:54 ] @
Darko, samo da ti skrenem pažnju da ti tražiš silu kojom treba da radiš bending, a to je komplikovanije nego da tražiš otklon da bi dobio odgovarajući ton.
Recimo, ja na svojoj gitari imam ove žice.
Kao što vidiš, svaka od njih ima drugačiju silu zatezanja.
Mislim da je najbolje da se i dalje oslanjaš samo na sluh, a da zaboraviš fiziku dok sviraš... [ darkosos @ 01.09.2012. 12:31 ] @
Fair enough... Ja koristim ove Gibson PURE, dakle za elektricnu gitaru. Pa, sto rece, ostaje mi da se usavrsavam :) [ djoka_l @ 01.09.2012. 12:59 ] @
Evo, na osnovu formula koje smo ostavili zzzz i ja može nešto da se i računa:
Recimo, da bendingom dobiješ notu koja je dva polu tona iznad osnovnog tona. Pošto u oktavi ima 12 polu tonova, a odnos frekvencija u oktavi je 1:2, za dva polu tona imaš da je f1:f=7:6
Ako pretpostavimo da je promena dužine zanemarljiva, kao i podužna masa nepromenljiva, tada je odnos rezultujućih sila zatezanja

pa je F1=49/36F
Tako imamo da je, na primer za D žicu F=70N, F1=95.28N.
Naravno, pošto svaka žica ima drugačiju silu zatezanja, sila kojom se deluje na žicu mora da bude drugačija. Ono što je isto je koeficijent 49/36 (uz gornje uslove).
Kada sviraš, ti ne meriš tih 49/36 nego imaš audio feedback i pokušavaš da dobije 7/6 od osnovnog tona. [ ac1bd4 @ 01.09.2012. 23:32 ] @
Probaj AP Tuner, besplatan i brz, a može dobro da posluži za utvrđivanje potrebnog otklona.  Sad to što se mora naučiti napamet za dalju upotrebu to je druga priča jer kada je potrebno brzo to izvesti stvarno nema šanse slušati pa se zaustaviti kada treba. [ darkosos @ 03.09.2012. 08:09 ] @
@djoka_I
Hvala na trudu, ja sam nesto pokusavao i bas se i jesam zapitao oko te uzduzne mase itd... Bas cu da probam taj rezultat koji si naveo. Ono sto je odmah jasno, a to sam i ja zeleo da proverim, je da na taj nacin sila ne zavisi od mesta na kome se vrsi bending! Dakle, to sto izgleda da je lakse to uraditi npr. na 15 pragu nego na 7 je posledica ili toga sto ova zanemarivanja nisu tako zanemarljiva (uglovi koje sam crtao su manje nezni sto je mesto blize kraju zice) ili je po sredi neko drugo svojstvo instrumenta/izvodjaca (sirina vrata, blizina kraja vrata - posebno za prvu zicu, polozaj ruke, da li sam pre toga prao sudove itd.)
Svakako je korisno, makar i za jednu zicu, a ono sto je zanimljivo je poveriti da li otklon ima neku invarijantu u odnosu na silu zatezanja. Mada, koliko vidim, sila zatezanje, zavisno od tipa zice, ne mora toliko da varira, jer se za nize tonove koriste deblje zice. Mozda cak vredi probati komplet koji ima sto vise izbalansirane ove sile... To naravno ako sviras stil u kome ima puno bendinga.
@ac1bd4
Mislim da sam koristio neko vreme AP Tuner, fin je to programcic, ali sada koristim "fizicki" tuner, koji se zakaci na telo gitare i ima mod u kome reaguje na vibracije samog tela, sto je vrlo zgodno.
[ djoka_l @ 03.09.2012. 09:18 ] @
Citat: Ono sto je odmah jasno, a to sam i ja zeleo da proverim, je da na taj nacin sila ne zavisi od mesta na kome se vrsi bending! Dakle, to sto izgleda da je lakse to uraditi npr. na 15 pragu nego na 7 je posledica ili toga sto ova zanemarivanja nisu tako zanemarljiva (uglovi koje sam crtao su manje nezni sto je mesto blize kraju zice) ili je po sredi neko drugo svojstvo instrumenta/izvodjaca (sirina vrata, blizina kraja vrata - posebno za prvu zicu, polozaj ruke, da li sam pre toga prao sudove itd.)
OK, ja sam malo varao u onoj formuli. Prvo, dužina L se povećava kada saviješ žicu, a podužna masa se smanjuje (jer je ista masa žice razvučena na veću dužinu). Međutim, ova dva efekta imaju suprotno dejstvo, povećavanje dužine smanjuje frekvenciju, a smanjenje podužne mase je povećava, pa sam ja (neopravdano) pretpostavio da se u krajnjem rezultatu ova dva efekta poništavaju, a krajnji rezultat zavisi samo od promene sile zatezanja.
Drugo veliko uprošćavanje je što sam računao samo rezultujuću silu zatezanja, a ona se dobija kada se uradi ono što si ti računao, tj. sila bendinga se razloži na komponente koje su u pravcu žice. Naravno, razlika kod bendinga na petom i 10 pragu je to što je žica više "asimetrična" na 5 pragu, pa je potrebna veća sila da se savije onaj deo žice od praga do vrha vrata nego donji deo.
[ darkosos @ 07.09.2012. 18:25 ] @
Da li moze ovako:
Pretpostavka bi bila da je sila zatezanja svuda jednaka prilikom zavijanja zice, odnosno kao da smo razvukli zicu za to koliko je ukupno razvucena u ona dva dela zice sa slike (AS + BS);
ovo bi izgleda znacilo da tacka C zaista nije otisla u S, sto je bilo jedno od mojih pitanja - dakle kao da je zica malo i skliznula sa prsta...
Ovakva pretpostavka bi nam omogucila da jednostavno izracunamo silu deformacije formulom 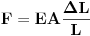 gde je E Jangov moduo, A povrsina preseka zice.
Dakle, napregnutost zice T je ovaj F + ono sto pise u specifikaciji zice, kada je u stimu.
Ono sto mi je malo pod znakom pitanja je da li sada mozemo da kazemo da u tacki S imamo silu T u smeru SA kao i u smeru SB? Tako bi bilo da je u liniji... u svakoj tacki (osim A i B) bi trebalo da imamo ove dve sile suprotnog smera, koje se ponistavaju. Jedino sto se u ovom slucaju ne ponistavaju, vec stvaraju rezultantu. To je ta sila koja se savladjuje prstom, zapravo. Posto bi onda onaj paralelogram sila bio romb, ta rezultanta bi bila malo otklonjena od pravca normale na zicu ( 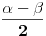 ). Ostalo bi da se izracunaju komponente na normalu i onaj deo koji je paralelan sa zicom. [ darkosos @ 15.09.2012. 21:53 ] @
Vidim da nema nesto interesovanja, ali u medjuvremenu sam uspeo da iskujem neku formulu za otklon zice. Bilo bi lepse kada bi mogla da se sredi tj. pojednostavi, jer otklon daje u implicitnom obliku a nisam imao volje ni da pokusam da resim eksplicitno.
Vrednosti koje sam dobio preko programa koji trazi nule zadate funkcije se poklapaju sto onim sto sam uspeo da izmerim. Uslovi svakako nisu previse naucni :), ali eto.
Elem, to izgleda nekako ovako:
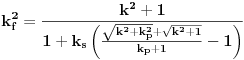
gde je kf kolicnik frekvenci pre i posle bendinga, k je odnos otklona i dela zice od praga na kome se vrsi bending do kobilice (CS/CB sa slike), ks je "koeficijent zice": 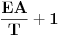 ( T je sila zatezanja zice u stimu, E Jangov moduo, A povrsina preseka zice) i konacno, kp je "koeficijent praga": odnos AC/BC.
Ono sto ova formula treba da da je zapravo to k, jer se na osnovu toga lako dobija otklon zice (CS=k*CB).
Ne znam da li ce ovo nekad nekog da zainteresuje, ali eto nek' stoji. Ne kazem da nisam negde pogresio, ali rezultati koje dobijam su solidni. Ako neko zeli, mogu da pokazem izvodjenje :) [ atelago @ 17.09.2012. 07:08 ] @
Na usmenom ispitu iz matematike profesor je tražio da prikažem ceo izvod
titranja žice po Dalamberu. Sada se ne sećam ni slovca od tog izvoda, ali
se sećam da je izvod bio toliko obiman da sam morao da obrišem tablu i da
nastavim tako da sam je još jedamput ispisao.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|