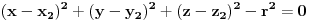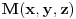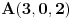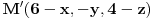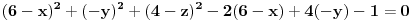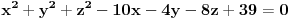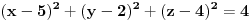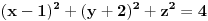[ smorilasamse @ 05.09.2012. 13:08 ] @
|
| Kaze zadatak : Naci jednacinu sfere koja je simetricna sferi S:x^2+y^2+z^2-2x+4y-1=0 u odnosu na tacku A(3,0,2)....... Ako su simetricne onda bih centar trazene sfere nasla pomocu Sredisne tacke, a ne znam da li treba da obrazujem novu ravan? Ima li neko ideju? |
[ djoka_l @ 05.09.2012. 13:23 ] @
A što bi ti trebala ravan. Sfera je centralno simetrična u odnosu na svoj centar. Nađi centar i poluprečnik sfere. Onda nađi centar druge sfere koji je simetričan centru prve sfere u odnosu na tačku A. Napiši jednačinu simetrične sfere koja ima isti poluprečnik kao i prva sfera, a centar koji si izračunala u prethodnom koraku...
Hint:
Jednačina prve sfere: 
Jednačina druge sfere: 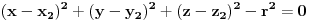 [ smorilasamse @ 05.09.2012. 14:26 ] @
znaci to je to.. kad uradis sto tezih zadataka,ne mozes da se setis najednostavnijih stvari. Hvala.
[ smorilasamse @ 05.09.2012. 15:08 ] @
odrediti projekciju presecne tacke pravih p i q [nasa sam tu racku ,ima koordinate M(3,2,7)] na ravan yOz.
e sad.. normalni vektor te ravni je (1,0,0) { ravan: x+D=0}
Moje pitanje je,da li mogu da uzmem bilo koji broj za D?
[ djoka_l @ 05.09.2012. 18:32 ] @
Meni se čini da si malo "prevežbala" zadatke, pa samo primenjuješ naučene formule bez razumevanja.
Ako je u pitanju y0z ravan, tada je jednačina ravni x=0, tj. D može da bude samo 0. Kada bi D bilo različito od nule, to bi bila ravan paralelna sa y0z pomerena za -D u smeru x ose.
[ smorilasamse @ 05.09.2012. 21:05 ] @
u pravu si,znam napamet sve,nista ne kapiram.. jbg. jel dajes casove?
[ miki069 @ 06.09.2012. 21:44 ] @
Analiticka geometrija i jeste oblast gde bas dosta mora da se zna napamet. Vrlo malo razmisljanja, jer se skoro sve radi po sablonu. Sablon znas ili ne znas. Niko od nas ga nije smislio. Postoje vec dugo. Na ispitima su uvek sablonski zadaci.
[ Nedeljko @ 06.09.2012. 22:46 ] @
Joj, šta mi napriča. Zavisi na kojim ispitima i gde. Ma, da, nema šta da se razmišlja. Tako sam ovih dana mučio muku da objasnim studentu da je vrlo bitno šta piše u zadatku, a jok da se radi bez razumevanja.
Evo ti ga jedan zadatak koji ima elegantno rešenje: Ispitati da li postoji familija međusobno mimoilaznih pravih koje ispunjavaju ceo prostor.
Što se tiče sfere simetrične sferi:
Tačka simetrična tački 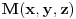 u odnosu na tačku 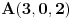 je tačka 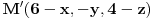 i obrnuto.
Šta je potreban i dovoljan uslov da tačka 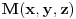 pripada sferi simetričnoj sferi  ? Pa, da njoj simetrična tačka 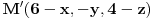 pripada sferi  . Dakle,
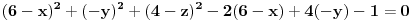
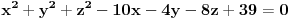
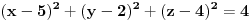 .
Inače, jednačina sfere  ima oblik
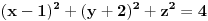 .
Ovo je opšti postupak, koji je primenljiv na bilo koju površ. [ smorilasamse @ 06.09.2012. 23:10 ] @
kome sad ja da verujem?:D
[ miki069 @ 06.09.2012. 23:37 ] @
Sablon koji znas ili ne znas. Ako ga ne znas unapred, tesko da ces ga ti smisliti. Razumevanje je pozeljno. Mislim na ispite na svim fakultetima, ukljucno MATF u Beogradu.
[ Nedeljko @ 06.09.2012. 23:55 ] @
Eto ti pa mi reši onaj zadatak sa tim svojim šablonima.
Ja kad sam polagao, mogao si najviše 50% da uradiš na šablon.
Kada razumeš šta radiš, svi ti šabloni na koje misliš sami ispadaju logično. Oni su prosta primena definicija.
Evo ti još jednog zadatka, koji sam radio kada sam spremao prijemni: Šta je geometrijsko mesto tačaka u ravni iz kojih se elipsa te ravni vidi pod pravim uglom?
[ Sonec @ 07.09.2012. 08:02 ] @
@miki069
Analiticka geometrija predstavlja oblast matematike koja se meni svidela upravo zato sto nema sablona. Zaista, dovoljno je u vecini slucajeva samo nacrtati sliku i sve ce nam se samo kasti.
Mislim da samo osobe sa skuvanim mozgom mogu da kazu da je ona sablonski predmet.
A to "ukljucno MATF u Beogradu" mozes da okacis macku o rep.
[ pexxi92 @ 07.09.2012. 09:24 ] @
Pa koja je to oblast matematike gde radis samo po sablonima bez razmisljanja?
[ Nedeljko @ 07.09.2012. 09:57 ] @
To "ako ne znaš šablone, teško ćeš ih se setiti" znači da ne znaš definicije ili eliminaciju parametara, a eliminacija parametara nema veze sa geometrijom. Primer eliminacije parametara je naći skup vrednosti funkcije ili odrediti parametre jednačine za koje ona ima ovakva ili onakva rešenja itd.
[ miki069 @ 07.09.2012. 19:36 ] @
Elipsa se vidi pod uglom od 90 stepeni iz svih tacaka centralne kruznice poluprecnika koren(a^2 b^2), gde su a i b ose elipse. Zadatak uradjen u 5 redova. Nikakva slika, nikakvo razmisljane. Uslov dodira, uslov normalnosti tangenti. Onda ko ne zna Vijetove formule racun ide na 5 strana, ko ih zna ide u 5 redova.
[ Nedeljko @ 07.09.2012. 20:20 ] @
Odlično! E, sad, koji su tu šabloni primenjeni? Da, postoje formule za uslov dodira, uslov normalnosti itd. Ali, ko ne razume šta radi, taj zadatak ne može da uradi.
E, sad me zanima onaj o familiji međusobno mimoilaznih pravih koje ispunjavaju ceo prostor.
Takođe, ima još jedan vrlo zanimljiv zadatak - da se dokaže da ako neki skup tačaka u prostoru ima osobinu da mu je presek sa svakom ravni prostora ili kriva drugog reda ili unija dve komplanarne prave ili prava ili tačka iliprazan skup, da je onda taj skup tačaka neka od površi drugog reda.
Oba su rešena ovde na ES.
Evo još jednog, koga nema ovde na ES.
Pod upisanom elipsom u trougao smatramo elipsu koja svaku ivicu trougla dodiruje u središnjoj tački te ivice.
a) Dokazati da se u svaki trougao može upisati tačno jedna elipsa.
b) Ako sve dešava u kompleksnoj ravni, a temena trougla koreni nekog polinoma trećeg stepena sa kompleksnim koeficijentima, onda su žiže elipse upisane u trougao koreni izvoda tog polinoma.
[ zzzz @ 08.09.2012. 11:26 ] @
@Nedeljko:Evo ti ga jedan zadatak koji ima elegantno rešenje: Ispitati da li postoji familija međusobno mimoilaznih pravih koje ispunjavaju ceo prostor.
Čemu služe ovakvi zadaci?Ako su pojmovi:tačka, pravac,ravan i prostor geometrijski aksiomi,da li se ovakvim zadacima dodatno pojašnjavaju ti pojmovi?
Naprimjer ovako:Ispitati da li postoji familija međusobno nepodudarnih tačaka koje ispunjavaju ceo dati pravac.
U fizici je neophodno osnovne pojmove objasniti posljedicama koje izazivaju jer nema boljeg načina.
[ Nedeljko @ 08.09.2012. 12:36 ] @
Zadatak je vrlo jasan, a nepodudarne tačke ne postoje.
Pojmovi tačaka i pravih jesu polazni u većini aksiomatizacija geometrije, ali između njih ne vladaju proizvoljni odnosi, već oni koji su određeni aksiomama. No, u zadatku se ne traži izvođenje rešenja u nekom konkretnom aksiomatskom sistemu, već bilo kako, tj. ako se podrazumeva da znamo zasnivanje geometrije i sve teoreme koje se uče u školama i na fakultetima, kako bi se rešio zadatak.
A svrha ovih zadataka je da se preispita stav o analitičkoj geometriji kao šablonskoj oblasti. Ovaj zadatak ima interesantno analitičko i interesantno sintetičko rešenje.
[ darkosos @ 10.09.2012. 07:51 ] @
Citat: zzzz:
U fizici je neophodno osnovne pojmove objasniti posljedicama koje izazivaju jer nema boljeg načina.
Zasto je to najbolji nacin? Meni bas smeta to sto su osnovni pojmovi promenljiva kategorija koja zavisi od znanja o posledicama...
EDIT: Sad sam shvatio koliko je ovo van teme :) [ zzzz @ 10.09.2012. 19:12 ] @
Citat: zzzz: @Nedeljko:Evo ti ga jedan zadatak koji ima elegantno rešenje: Ispitati da li postoji familija međusobno mimoilaznih pravih koje ispunjavaju ceo prostor.
.
Niko ne pokušava.Koga interesuje rješenje može pogledati ovdje:
http://www.elitesecurity.org/p333295[ Nedeljko @ 10.09.2012. 21:47 ] @
Možda niko nije znao. No, dobro, to je to.
[ smorilasamse @ 13.09.2012. 09:28 ] @
Citat: smorilasamse:
odrediti projekciju presecne tacke pravih p i q [nasa sam tu racku ,ima koordinate M(3,2,7)] na ravan yOz.
e sad.. normalni vektor te ravni je (1,0,0) { ravan: x+D=0}
Moje pitanje je,da li mogu da uzmem bilo koji broj za D?
sad cu da obrazujem pravu koja prolazi kroz tacku M i ciji je vektor (1,0,0) , pa cu napisati pravu u parametarskom obliku, pa cu to sve ubaciti u ravan x=0, i sta dobijem za parametar to vratim u parametarsku jednacinu prave,i to je biiti projekcija presecne tacke? [ Nedeljko @ 13.09.2012. 09:36 ] @
I dobićeš tačku M'(0,2,7).
[ smorilasamse @ 13.09.2012. 09:46 ] @
Da,to sam dobila. Hvala .
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|