Ako je x-y=d,supstitucija x=y+d,pa kad riješim kvadratnu jednačinu,dobijem :
y(1)=2d+korijen iz(d(6d+1))
:y(2)=2d-......
Diskriminanta d(6d+1) treba imati cijelobrojan korijen.Faktori su relativno prosti
pa d treba da je kvadrat cijelog broja.

Ali mora biti ispunjen i uvjet da je 6d+1 takođe kvadrat cijelog broja.To ide ako je
d=4 pa je y(1)=18;x(1)=22 i y(2)=-2;x(2)=2.(0vaj drugi par ne upada u skup
prirodnih br.)

Diskusiju o diskriminanti namjerno sam preskočio.

E ali sad ja postavljam pitanje:Dokazati da je x-y=4 jedino rješenje!
(Priznajem da to nisam do kraja izanalizirao)

Postoji više rešenja, recimo:
4, 400, 39204, 3841600, 376437604, 36887043600, ...

Kažeš da d i (6d + 1) moraju biti kvadrati, znaci neka je a na kvadrat jednako d, a b na kvadrat jednako (6d + 1). Uz sve to, a i b su nam prirodni brojevi.




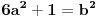
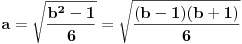
Jedan od činilaca pod korenom mora da bude deljiv sa 6 i ceo izraz pod korenom mora da bude kvadrat jer je a prirodan broj...

Ovih nekoliko rešenja sam programski isterao. Postoji li formula za opšti član niza rešenja?

Preuređivanjem izraza dobijamo:



Prema ovome, biće dovoljno da pokažemo da je pun kvadrat. Da bismo to uspeli, pokazaćemo da su brojevi i uzajamno prosti. Pretpostavimo suprotno, da imaju zajednički činilac :

;
;
, što je nemoguće za . Dakle, brojevi i su uzajamno prosti, pa njihov proizvod može biti pun kvadrat samo ako su i oni sami puni kvadrati. QED