Ako si se bas nameracio da to dokazes matematicki, probaj sa matematickom indukcijom...

pa mozda moze i ovako :)
Teorija: Proizvod tri sukcesivna (uzastopna) prirodna broja je uvijek djeljiv sa tri.
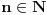
Prema gore navedenom, treba dokazati da se gorinji izraz ili njegov dio moze prikazati kao proizvod tri sukcesivna prirodna broja. Pretpostavljamo da je u uslovima zadatka . Prema tome imamo:

*
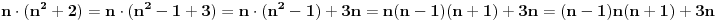
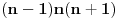
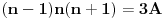
pošto izraz predstavlja proizvod tri sukcesivna prirodna broja, to je on djeljiv sa 3 pa stoga možemo pisati gdje je

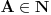
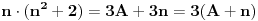
Na kraju se izraz * može napisati kao što je svakako djeljivo sa 3 jer je jedan faktor upravo broj 3. That's it without mathematical induction :)

Uradio sam indukciojom.

1. Provjera za n = k
2. Pretpostavka da je tacno za n = k
3. Dokaz da je tacno za n = k + 1

Hvala svima.

Ispravka: u prvom koraku je provjera za n = 1.

Kolinsovo resenje je svakako lepse... Moj komentar je bio samo u vezi "matematicki dokaz", nek' mi MrNash oprosti :) Jer ne znam kako bi ovo drugacije dokazao sem matematicki, ali ne neophodno matematickom indukcijom, kako mi se cini da je Kolins razumeo moj komentar... U svakom slucaju, to je to, 'vako il' 'nako...

Ma nema u matematici lijepih rješenja hehehehe šalim se naravno. Ukoliko se nešto može uraditi bez "više" matematike, uvijek ću prednost dati tom rješenju ovdje, jer su "korisnici" ovih rješenja i učenici npr. osnovnih škola, a oni ne znaju za pojam matematičke indukcije. Čak štaviše, ja sam matematičku indukciju učio u IV razredu srednje škole, i prema planovima i programima za većinu srednjih škola u BiH, indukcija se i uči u IV razredu (možda je izuzetak matematička gimnazija i srodne škole gdje se mat. indukcija izučava u ranijim razredima). MrNash ti nama još uvijek nisi pokazao kako si ovo dokazao matematičkom indukcijom. Ti si samo napisao korake koje treba odraditi, tj. nekakvu hajmo reći, teoriju :) Slobodno napiši i svoje rješenje, nekom će pomoći :)

Evo ga:

1. Provjera za n = 1 vam je jasna
2. n = k je pretpostavka
3. Dokaz za n = k + 1

n*(n*n+2) = n^3 + 2n

(k+1)^3 + 2*(k+1)=

k^3 + 3k^2 + 3k + 1 + 2k + 2 =

(k^3 + 2k) + 3 + 3k^2 + 3k

Prvi sabirak (k^3 + 2k) je djeljiv sa 3 iz pretpostavke pod brojem 2 (za n = k),
svi ostali sabirci su ocigledno djeljivi sa 3 pa samim tim i zbir je djeljiv sa 3.