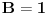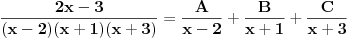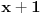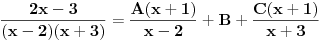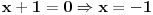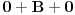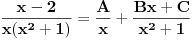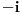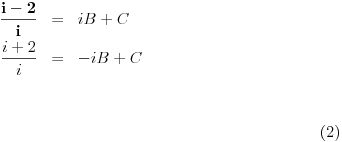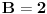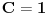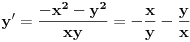[ kikik @ 19.09.2012. 12:34 ] @
| Vježbam neki zadatak koji izgleda ovako Integral (1+2x)/(x^4+2x^3+2x^2+x) dx E sada pošto je u pitanju prava racionalna funkcija nju izdvajam i rastavim, i dobijem sljedeće x^4+2x^3+2x^2+x = x(x^3+2x^2+2x+1) = x(x+1)(x^2+x+1) I sada radim integral kao 1+2x / x(x+1)(x^2+x+1) odnosno A/x + B/x+1 + Cx+D/x^2+x+1 = 1+2x *** Nisam baš siguran da sam ovo dobro postavio Cx+D? Poslije kada ovo rješim dobijam A=1 C=-1 B=1/2 D=-1/2 I onda idem dalje kao: integral 1dx/x + integral 1/2 / x+1 dx - integral x-1/2 / x^2+x+1 I to poslije rješim. Poslije sam htjeo da provjerim jel to dobro i rješio sam integral u alphawolframu i on daje drugačiji rezultat, pa ako neko može da mi kaže gdje grješim? |