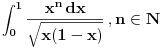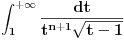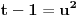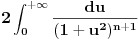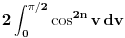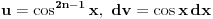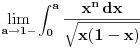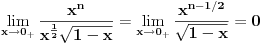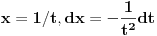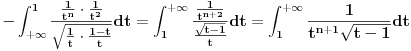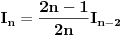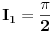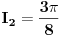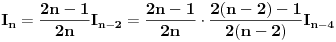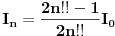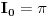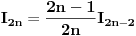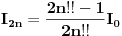[ pitomir @ 20.09.2012. 09:30 ] @
|
[ Sonec @ 20.09.2012. 09:48 ] @
A zbog cega nije singularitet u nuli?
[ pitomir @ 20.09.2012. 09:54 ] @
Nama je asistent rekao da ako postoji konacan limes podintegralne funkcije kada tezi nuli (na primer), onda nula nije singularitet. A recimo u Krtinicevoj skripti pise da je tada nula otklonjiv singularitet, sta god.
[ Sonec @ 20.09.2012. 10:06 ] @
[ pitomir @ 20.09.2012. 10:13 ] @
[ pitomir @ 20.09.2012. 10:20 ] @
Da, ide parcijalna, pa posle smena cos x = t, i na kraju dobijem rezultat -2 :)
Hvala! [ Sonec @ 20.09.2012. 10:29 ] @
[ pitomir @ 20.09.2012. 10:33 ] @
Au, da, parcijalna mi nije dobra :/
[ Nedeljko @ 20.09.2012. 10:39 ] @
Rimanov integral se definiše na domenima merljivim po Žordanu, recimo pozitivne mere i postoji akko je podintegralna funkcija ograničena i ima skup tačaka prekida Lebegove mere nula. Dakle, za ma koje
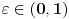 Rimanov integral date funkcije na intervalu Rimanov integral date funkcije na intervalu 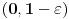 , koji je merljiv po Žordanu. , koji je merljiv po Žordanu.U slučaju Lebegovog integrala, nesvojstveni integral se ne definiše, jer Lebegov integral nema problem sa singularitetima. Svaki apsolutno konvergentan nesvojstveni integral postoji kao običan Lebegov integral. Smenu 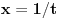 nisi uvela dobro. Izložilac treba da ti bude manji za jedan. nisi uvela dobro. Izložilac treba da ti bude manji za jedan.Dalje, probaj parcijalnom integracijom integrala 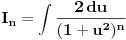 da odrediš vezi između  i i 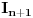 , a onda izrazi , a onda izrazi 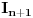 preko preko  . .[ Sonec @ 20.09.2012. 10:59 ] @
[ pitomir @ 20.09.2012. 11:15 ] @
[ Sonec @ 20.09.2012. 11:22 ] @
[ pitomir @ 20.09.2012. 11:35 ] @
[ Sonec @ 20.09.2012. 11:47 ] @
Ja nisam siguran da si dobro uradila parcijalnu integraciju, tacnije, msm da je umesto
 trebalo da stavis trebalo da stavis 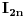 . Pa se onda drugacije ponasa rekuretna formula. . Pa se onda drugacije ponasa rekuretna formula.Ja sam na Uvodu u matematicku logiku ucio da 0 jeste prirodan broj. Seti se samo kod uvodjenja prirodnih brojeva: prvo definisemo nulu, a zatim na osnovu nje i jedan, a preko nule i jedinice definisemo dva itd. Inace, nisi lepo sredila sa dvostrukim faktorijelom. (al ipak msm da treba da bude  , prvo to da utvrdimo). , prvo to da utvrdimo).[ pitomir @ 20.09.2012. 11:51 ] @
Jao, jeste, 2n je definitivno trebalo. Nista, ispocetka cu.
Jeste, logicari smatraju nulu prirodnim brojem, a matematicari ne. Secam se profesora iz linearne kad ga je neko od nas pitao da li je nula prirodan broj, kaze ne, ne, nikako. [ Sonec @ 20.09.2012. 11:54 ] @
Pa valjda su i logicari matematicari. Cela matematika se zasniva na logici.
Al da, svakako, zavisi kako ko tumaci. [ pitomir @ 20.09.2012. 12:04 ] @
[ Sonec @ 20.09.2012. 12:16 ] @
Najlakse nam je bilo da smo racunali integral kada je na
 , umesto , umesto  , i kada dobijemo tu formulu, umesto , i kada dobijemo tu formulu, umesto  stavimo stavimo  . I trebalo bi da bude . I trebalo bi da bude  , ne , ne 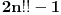 . .Pretpostavljam da ti je profesor bio Nebojsa Ikodinovic, posto je i nama (mojoj grupi) isto tako obelezavao. Za nulu imas i temu http://www.elitesecurity.org/t442394-0 Ukucaj u search improper integral ovde http://www.artofproblemsolving.com/Forum/search.php i eto ti jos zadataka za vezbu. (sta bih dao da sam znao za ovaj sajt pre godinu dana) [ pitomir @ 20.09.2012. 13:00 ] @
[ Sonec @ 20.09.2012. 13:14 ] @
A da nije mozda
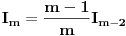 ? ?Inace (ako nisi znala) evo ti sta je dvostruki faktorijel http://www.elitesecurity.org/t158909-0#1034100. A ti primeti da je u tvom slucaju  parno. parno.[ pitomir @ 20.09.2012. 13:27 ] @
[ Sonec @ 20.09.2012. 13:35 ] @
[ pitomir @ 20.09.2012. 13:38 ] @
Ne, nisam zamenila m = 2n (zaboravila sam).
[ Sonec @ 20.09.2012. 13:49 ] @
Malo sam napravio konfuziju jer sam promenio poruku, moja greska.
Dobro je resenje. Ne treba nista da mi odgovaras sta ti predstavlja 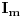 , ja sam se nesto zbunio. , ja sam se nesto zbunio.Wolframovo resenje (ne razumljivo za tebe, verovatno (jer se Gama funkcija radi u 2 godini)) je 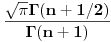 , sto je (s obzirom da je , sto je (s obzirom da je  prirodan broj) jednako: prirodan broj) jednako: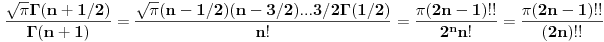 Koristio sam da je 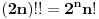 [ pitomir @ 20.09.2012. 14:08 ] @
Ok, nema veze, bitno da smo se razumeli.
Pominjali smo Gama funkciju na vezbama, ali nismo se udubljivali, posto to sigurmo nece biti na ispitu. Hvala ti puno, bas mi je znacilo! Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|