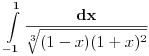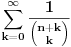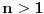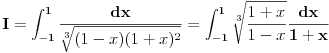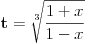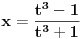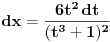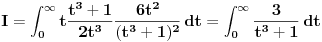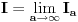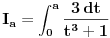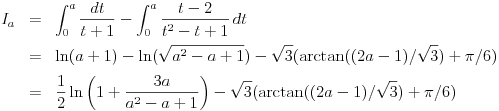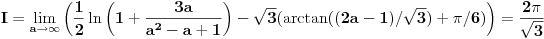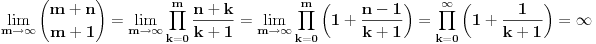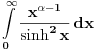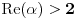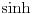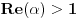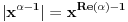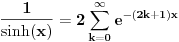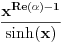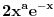[ Sonec @ 25.09.2012. 12:23 ] @
|
[ Nedeljko @ 25.09.2012. 20:34 ] @
[ Sonec @ 25.09.2012. 20:52 ] @
Prvi je dobar, mada sam na umu imao drugacije resenje, pa cu sacekati jos malo dok ga ne pokazem, mozda se neko drugi seti.
Drugi ti nije dobar, tacnije, skoro si isterao do kraja (mada i tu imam drugacije resenje), samo si pogresio prilikom pustanja limesa. [ Nedeljko @ 25.09.2012. 22:02 ] @
[ Sonec @ 25.09.2012. 22:10 ] @
Pa i jeste, al onda rezultat nije 1, jer imas i onaj deo i ispred zagrade koji ne zavisi od m.
[ miki069 @ 25.09.2012. 22:17 ] @
Nedeljko svaka čast za integral.
Za drugi Excel pokazuje da je tačan rezultat cele sume n/(n-1), a to je tačno ono što Nedeljko i ima ispred zagrade. Bravo i za drugi. [ Sonec @ 25.09.2012. 22:49 ] @
Nedeljko je rekao sledece:
Citat: Nedeljko: Kada to znamo, nije teško zaključiti da je cela suma jednaka jedinici. A kako konacno resenje nije 1, to onda svakako nije tacno. Pa sam zbog toga rekao (mada se mora priznati poprilicno traljvavo, jer sam apelovao na limes misleci na kraj): Citat: Sonec: Drugi ti nije dobar, tacnije, skoro si isterao do kraja (mada i tu imam drugacije resenje), samo si pogresio prilikom pustanja limesa. I onda je Nedeljko (zbog moje traljavosti) poceo da pokazuje da je odgovarajuci limes binomnog koeficijenta zaista  . .Da, konacno resenje jeste 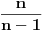 i to stoji ispred zagrade, ali je receno da je ono 1, pa se nije moglo uzeti za tacno. i to stoji ispred zagrade, ali je receno da je ono 1, pa se nije moglo uzeti za tacno.[ Nedeljko @ 25.09.2012. 22:54 ] @
U pravu si. Ja sam računao kao da i n teži beskonačnosti. Svašta!
[ Sonec @ 30.09.2012. 22:06 ] @
Smatram da sam vam dao dovoljno vremena da pokusate da uradite zadatke i na drugi nacin (u odnosu na Nedeljkovo resenje).
Meni su se veoma svideli zadaci jer imaju (za mene) lepa resenja. Verovatno je to i zato sto ja kada vidim Gama i Beta funkcije pobenavim sav i sve mi je lepo sto se radi sa njima. Moram reci da sam pretpostavio da ce se prvi zadatak uraditi na nacin koji je uradjen (mislim na Nedeljkovo resenje) jer sam vidjao vec na par mesta (mislim i na ovom forumu, moguce je da je bio isti integral) da se koristi taj "trik". Resenje koje cu ja predstaviti verovatno koristi smenu koja nije toliko ocigledna (zbog dvojke koja se pojavljuje), ali koja tako lepo preoblikuje integral da bi svako trebalo da moze da zavrsi sam zadatak (jer posle smene Beta funkcija naprosto "vristi" da se primeni). Da ne duzim mnogo, evo ih (jos neka) resenja. Kod prvog se uvede smena 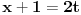 , ,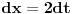 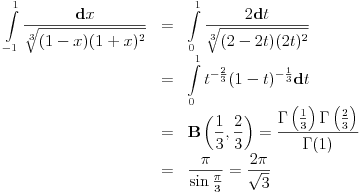 Kod drugog samo treba raspisati binomni koeficijenat, a zatim faktorijele zameniti sa Gama funkcijom, i onda se Beta funkcija sama namece i posle je lako 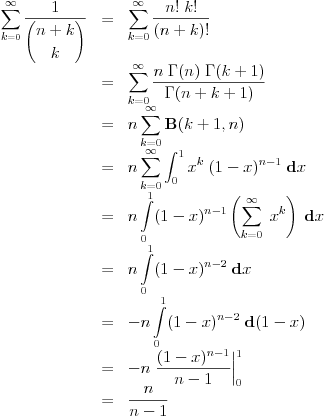 [ Nedeljko @ 30.09.2012. 22:31 ] @
Lepo, samo mislim da su moja rešenja direktnija i elementarnija. Naravno, primedba o omaški pri puštanju limesa stoji.
[ Sonec @ 30.09.2012. 22:44 ] @
To si u pravu.
[ Nedeljko @ 22.10.2012. 08:56 ] @
[ Sonec @ 22.10.2012. 09:52 ] @
Nedeljko, ovde je
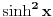 , ne , ne 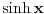 . .Ovo jeste tacan rezultat za integral 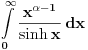 za za 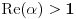 , ali to nije trazeni integral. , ali to nije trazeni integral. Inace, rezultat (za integral koji si ti resavao) se moze spakovati u jos jednostavniju formu, naime, 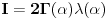 , gde je , gde je  Dirichlet Lambda Function. Dirichlet Lambda Function.I bilo bi lepo (ja to znam, al zbog ostalih koji budu citali jednoga dana) da ispises malo detaljnije resenje (za ovo sa 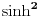 ),u smislu, zasto je dati razlomak sa sinus hiperbolickim jednak bas takvoj sumi, i sam integral kad se svodi na Gama funkciju, znas vec, ako nemas vremena ni zelje, ispisacu ja. ),u smislu, zasto je dati razlomak sa sinus hiperbolickim jednak bas takvoj sumi, i sam integral kad se svodi na Gama funkciju, znas vec, ako nemas vremena ni zelje, ispisacu ja.[ Nedeljko @ 22.10.2012. 12:50 ] @
Pa, ništa,
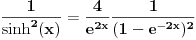 . .Za 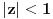 važi važi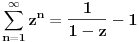 . .Stepeni redovi se unutar oblasti konvergencije mogu diferencirati član po član, pa je 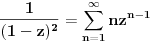 . .Otuda je 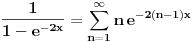 za 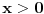 . Odatle sledi da je . Odatle sledi da je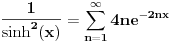 . .Pritom se polazni integral posle te zamene može integraliti član po član, jer je 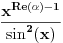 integralna dominanta. Kada je integralna dominanta. Kada je  pozitivno i blisko nuli, dominanta se ponaša kao pozitivno i blisko nuli, dominanta se ponaša kao 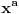 za za 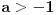 , a u okolini beskonačnosti kao , a u okolini beskonačnosti kao 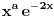 . .Integracijom član po član dobijamo da je 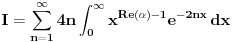 . .Uvođenjem smene 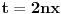 dobijamo konačno da je dobijamo konačno da je 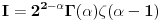 . .[ Sonec @ 22.10.2012. 18:50 ] @
[ Sonec @ 17.12.2012. 23:08 ] @
Izracunati:
1. 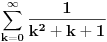 2. 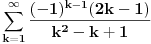 S tim da drugi zadatak ne znam (za sada :)) da uradim. Mozda moze da se uradi slicno kao i prvi, al ja ne vidim kako (nesto sam pokusavao, al slaba vajda). Jedino (izmedju ostalog) sto sam primetio je da je izvod imenioca jednak brojiocu (ako zanemarimo 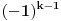 ), al to sumnjam da mnogo sta znaci. ), al to sumnjam da mnogo sta znaci. Ideja (koja je meni poznata) za resenje prvog zadatka nije ocigledna (kako kome), ali je samo resenje za mene lepo. [ zzzz @ 18.12.2012. 10:22 ] @
[ Sonec @ 18.12.2012. 18:09 ] @
Zbrzio si, dobija se
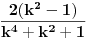 . Sve ovo konvergira, tako da smemo da razdvajamo sume, samo je sad problem, kako naci sumu ciji su elementi oblika . Sve ovo konvergira, tako da smemo da razdvajamo sume, samo je sad problem, kako naci sumu ciji su elementi oblika 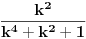 , moracu da razmislim malo o tome (a mozda se i neko seti), mozda da mu (kada je slucaj , moracu da razmislim malo o tome (a mozda se i neko seti), mozda da mu (kada je slucaj 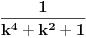 ) dodam ) dodam 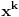 , pa onda diferenciranjem nesto da dobijem, al nesto sumnjam. Ovaj drugi deo nije problem izracunati, svodi se na prvi zadatak jer je , pa onda diferenciranjem nesto da dobijem, al nesto sumnjam. Ovaj drugi deo nije problem izracunati, svodi se na prvi zadatak jer je 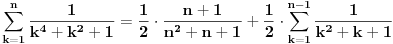 , pa se dobija , pa se dobija 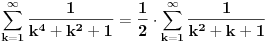 . .[ Nedeljko @ 29.12.2012. 09:49 ] @
I dobro, kako se radi prvi zadatak? Pokušao sam svašta, ali nisam uspeo.
[ pexxi92 @ 29.12.2012. 12:25 ] @
Pa za prvi zadatak mozda moze da se svede na dif. jednacinu drugog reda. Za drugi nisam siguran imam par ideja...
[ Nedeljko @ 29.12.2012. 13:27 ] @
Može i drugi da se svede na diferencijalnu jednačinu drugog reda. No, u oba slučaja se dobija nehomogena Ojlerova diferencijalna jednačina sa nehomogenim delom čija se integracija svodi na polazni red.
[ pexxi92 @ 29.12.2012. 13:31 ] @
Da za resavanje nisam bio siguran, ne znam toliko dobro diferencijalne jednacine pa nisam siguran dali za ove postoji analiticko resenje...
[ Sonec @ 29.12.2012. 18:38 ] @
Primetimo prvo da je
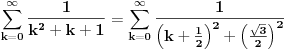 Koristicemo dobro poznat (za sinus pogotovo) identitet 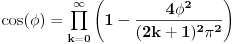 , koji ovom prilikom necemo dokazivati. , koji ovom prilikom necemo dokazivati.Logaritmujuci (ocigledno) obe strane dobijamo: 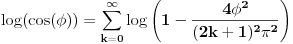 Diferencirajuci obe strane po  dobijamo: dobijamo: 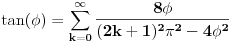 Neka je 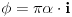 . Tada dobijamo . Tada dobijamo 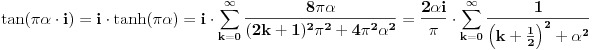 Dakle, nasli smo da je 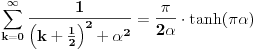 Sad je lako, stavimo 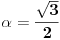 i dobijamo nas slucaj. Dakle, i dobijamo nas slucaj. Dakle, 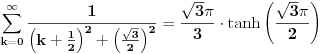 , odnosno , odnosno 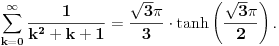 [ Sonec @ 23.02.2013. 10:53 ] @
Ova suma
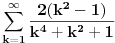 se moze naci vrlo lako. Ponekad ne treba bespotrebno petljati. Naravno, resenje je parcijalna dekompozicija izraza pod sumom. Naime, se moze naci vrlo lako. Ponekad ne treba bespotrebno petljati. Naravno, resenje je parcijalna dekompozicija izraza pod sumom. Naime, 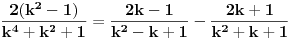 . Primetimo da je . Primetimo da je 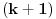 -vi clan oblika -vi clan oblika 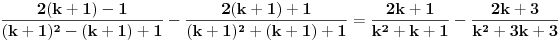 , tj. primecujemo pravilo kako se uzastopni clanovi u datoj sumi skracuju. Sada lako nalazimo da je , tj. primecujemo pravilo kako se uzastopni clanovi u datoj sumi skracuju. Sada lako nalazimo da je 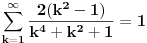 . .I neko bi sad rekao, odlicno, nasli smo polaznu sumu 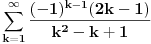 . E pa, prc, nismo, jer ne vazi . E pa, prc, nismo, jer ne vazi 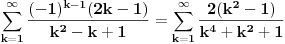 , ja sam pogresio u racunu tada. Naime, ideja razdvajanja na parove , ja sam pogresio u racunu tada. Naime, ideja razdvajanja na parove 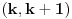 se ne moze primeniti tako da suma ostane da ide od se ne moze primeniti tako da suma ostane da ide od 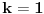 do do  . Moze da se razdvoji ali tako da indeksi idu po neparnim brojevima . Moze da se razdvoji ali tako da indeksi idu po neparnim brojevima 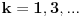 , onda bi bilo korektno, ali bi bilo zeznuto naci tu sumu. Ako bismo rastavili na parne i neparne clanove, dakle, oblika , onda bi bilo korektno, ali bi bilo zeznuto naci tu sumu. Ako bismo rastavili na parne i neparne clanove, dakle, oblika 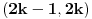 , onda bi , onda bi  islo lepo redom, ali bismo dobili komplikovaniju sumu, naime, tada bi vazilo islo lepo redom, ali bismo dobili komplikovaniju sumu, naime, tada bi vazilo 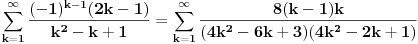 . Ali, treba ovo izracunati. . Ali, treba ovo izracunati.Al ako nista, za utehu, na ovaj nacin smo nasli sumu 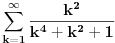 . Iz prethodnih razmatranja nalazimo . Iz prethodnih razmatranja nalazimo 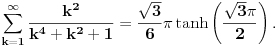 Ali uspeo sam da izracunam i pocetnu sumu, polazeci od pocetne sume 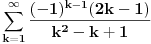 (dakle, sve ove modifikacije mi nisu bile od nekog veceg znacaja). Naime, iz mog prethodnog posta nalazimo (dakle, sve ove modifikacije mi nisu bile od nekog veceg znacaja). Naime, iz mog prethodnog posta nalazimo 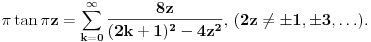 Iz transformacije 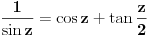 nalazimo dalje nalazimo dalje 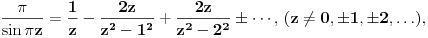 a zamenjujuci a zamenjujuci  sa sa 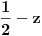 nalazimo nalazimo 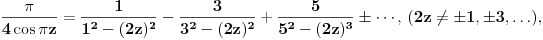 odnosno odnosno  . . Ovde je prakticno kraj, jer stavljajuci 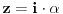 nalazimo nalazimo 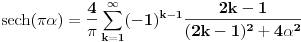 , a zatim stavljajuci , a zatim stavljajuci 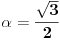 nalazimo nalazimo 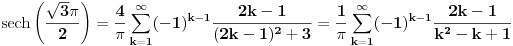 , odnosno , odnosno 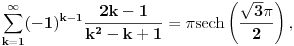 sto je i trebalo naci. sto je i trebalo naci. [ Nedeljko @ 24.02.2013. 15:48 ] @
E, alal ti kupus za ovo.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|