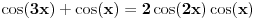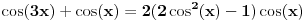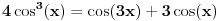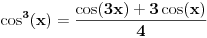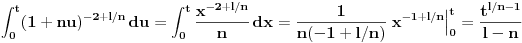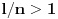[ kikik @ 26.09.2012. 19:01 ] @
|
| Rjesavam jedan određeni integral, tj. pokušavam da ga rjesim
Integral je u granicama od o do pi e^x sin^2 x cosx dx
Sada napisem da je sin^2 x = 1 - cos^2 x
I onda dobijem e^x cosx (1-cos^2 x) dx
Zatim dobijem e^x cosx - e^x cos^3 x dx
i onda to rastavim na dva odre]ena integrala u granicama od 0 do pi
e^x cosx dx - e^x cos^3 x dx
Sada nisam siguran kako da rjesim ovo dalje, pretpostavljam da bih trebao da uvedem neku smjenu u prvom integralu, a vjerovatno i u drugom? |
[ Nedeljko @ 26.09.2012. 20:20 ] @
Prvi integral radiš dva puta parcijalno, a što se drugog tiče, važi:
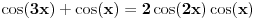
,
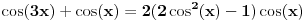
,
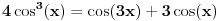
,
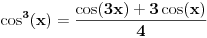
.
Je li sada lakše?
[ kikik @ 26.09.2012. 21:04 ] @
Prvi sam shvatio, prelagano je, ocito sam totalno zablokirao pri rješavanju maloprije, hvala :)
prvo pišem da je
u=cosx
du=-sinx dx
dv= e^x dx
v= e^x
pa zatim rješim to, i onda opet uradim parcijalnu i na kraju dobijem rezultat (e^x (sinx + cosx))/2
Ali i pored ove pomoći za drugi, ne mogu da skontam kako da uradim..
Prema ovome što si mi ti napisao dobijem integral od e^x * (cos3x + 3 cosx) /4 ... Konstantu mogu izvući ispred zagrade? I onda bi trebao da izvršim neku smjenu, mislim?
[ kikik @ 26.09.2012. 21:51 ] @
Mislim da sam ipak rjesio i ovaj integral :)))
[ kikik @ 29.09.2012. 22:25 ] @
Da ne otvaram novu temu..
Rjesavam odredjeni integral u granicama od 1 do 2 ∫e^2x cos(2x+3) dx
Sada sam uradio smjenu 2x=t dt=2dx dx=dt/2 i dobijem
1/2 ∫ e^t cos (t+3) dt
Sada nisam siguran sta da uradim i kako ovo da rjesim, pa ako moze mala pomoc :)
[ Nedeljko @ 30.09.2012. 02:09 ] @
Dva puta parcijalno.
[ miirsad @ 20.11.2012. 22:18 ] @
Kako ne bih otvarao novu temu , a nisam bas sa integralima na ti, molio bih za pomoc:
Integral je u granicama od o do t (1+nt)^(-2+l/n) dt
[ Nedeljko @ 20.11.2012. 22:44 ] @
Pošto izložilac ne zavisi od promenljive po kojoj se vrši integracija, smenom x=1+nt integral se svodi na tablični.
[ Nedeljko @ 20.11.2012. 22:54 ] @
E, da, nije zgodno da promenljivu po kojoj se vrši integracija označiš isto kao neku promenljivu koja učestvuje u granicama ili van integrala.
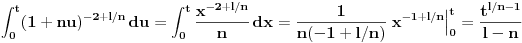
.
Naravno, sve za
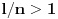
. U protivnom je integral bekonačan.
[ miirsad @ 21.11.2012. 05:56 ] @
Citat:
Nedeljko: E, da, nije zgodno da promenljivu po kojoj se vrši integracija označiš isto kao neku promenljivu koja učestvuje u granicama ili van integrala.
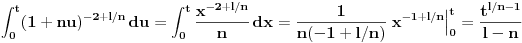
.
Naravno, sve za
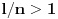
. U protivnom je integral bekonačan.
Hvala puno i svako dobro..
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.