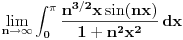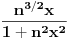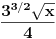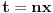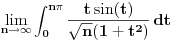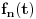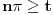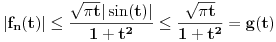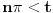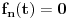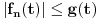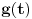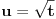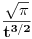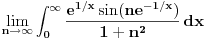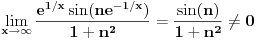[ pitagorina.teorema @ 28.09.2012. 10:42 ] @
| Potrebna mi je ideja za rješavanje zadatka lim (n → beskonačno) integral u granicama od 0 do pi (n na 3/2*x*sinnx)/(1+n na 2*x na 2) Obicno u ovakvim zadacima za dominantu, tj g(x) uzimamo nulu prvog izvod niza posmatranog kao f-ja argumenta ne uvrstenu u fn(x), medjutim kad imam sin previse se zakomplikuje i ne mogu da dobijem nulu prvog izvoda.. :/ |