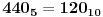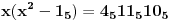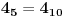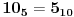Ako je osnova sistema 5, taj sistem sadrzi cifre: 0, 1, 2, 3, 4
Ne postoji 5. Ti si kao resenje dobio 5, sto znaci da je to sledeci broj posle 4, a u sistemu sa osnovom 5 taj broj je 10.
Razumes?

Edit: Tehnicki, tvoje resenje je iz baze 10. Moras vratiti nazad na bazu 5.

Hvala, shvatio sam to. Jos jedno pitanje. Sta u slucaju da dobijem rjesenje x=10. Sad sam rjesio jos 2 zadatka, u jednom sam dobio x=12 i pretvorio sam i dobio sam brojeve 22,23,24. U drugom zadatku sam dobio rjesenje x=10 i sad trebam se prebaciti u bazu 9. U rjesenjima pise da je rezultat 10,11,12 ? Znaci jednom sam se prebacio u drugi brojevni sustav a u slucaju 10 samo sam nastavio 11,12.

Ne. Uvek moras vratiti nazad u originalni sistem. U zadatku gde si dobio da je x=10₁₀ kada prebacis u osnovu 9 ispada da je x=11₉.
S obzirom da traze x-1, x, x+1 zato su resenja 10₉, 11₉, 12₉. Igrom slucaja je bilo takvo resenje da se x-1 zapravo pise kao 10₉. Ali imaj na umu da je to i dalje u bazom 9, znaci "nema veze" sa bazom 10.

Znas kako se vraca u originalnu bazu?
Celobrojno delimo broj iz baze 10 sa osnovom novo sistema gde ostatak pisemo nakon jednako, a ispod pisemo rezultat. Na kraju procitamo brojeve posle znaka jednakosti od dole ka gore.

Evo kratkog primera.

53₁₀ = X₈

53 / 8 = 5 <- pisemo ostatak
6 / 8 = 6
0 / 8 <- kraj

Resenje: X₈ = 65₈

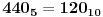
Najprostije je da i onda rešiš zadatak u dekadnom sistemu. Dobija se da su to brojevi 4, 5 i 6.

Može da se radi i u sistemu sa osnovom 5, ali onda sve računske operacije moraš vršiti u tom sistemu



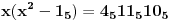
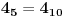
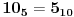
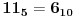
Obzirom da je , i , dobijamo da su to brojevi 4, 5 i 6.

Zahvaljujem, sad je sve jasno.