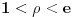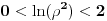[ kikik @ 09.10.2012. 14:16 ] @
| Radim neki zadatak pa sam malo zapeo, pa ako moze mala pomoc Izracunati integral po D ln^2(x^+y^2) / x^+y^2 dxdy gdje je D dio ravni ogranicen sa x^2+y^2=1, x^2+y^2=e^2 x=ro cos fi y=ro sin fi i onda dobijem da ro pripada od 1 do e, a fi pripada od o do 2pi Dalje kada radim imam odredjeni integral od o do 2pi dfi i odredjeni integral od 1 do e ln(ro^2 cos^2 fi + ro^2 sin^2 fi) / (ro^2 cos^2 fi + ro^2 sin^2 fi) ro d ro onda dobijem 2pi integral od 1 do e ((ln^2(ro^2) / ro^2) r d ro ) na kraju imam 2pi integral od 1 do e (ln^2(ro^2)/ ro) dr i onda napravim smjenu pa mi je ln(ro^2)=u, du=2*ro/ro^2 dro du=2/ro dr ... E sada nisam siguran da li sam ovu smjenu dobro odradio, tj. da li ide ovako i da li trebam da mjenjam granice ovog integrala poslije uvodjenja smjene? |