Da probam ovo prvo:

oznacicu poen igraca A (koji servira) sa 1, a igraca B sa 0; tako dobijam nizove 0 i 1, sa sledecim mogucnostima:

- niz od 4 uzastopna poena igraca A, 1111, sa verovatnocom p⁴;

- niz sa 4 jedinice i jednom nulom, koja ne sme biti na poslednjem mestu, dakle 5 -1 = 4 mogucnosti, sa verovatnocom

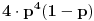
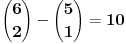
- niz sa 4 jedinice i 2 nule, koja dakle ne sme biti na poslednjem mestu, pa imamo , sa verovatnocom

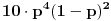
sada ulazimo u zonu izjednacenja (3 poena za igraca B je dakle 40 pravih poena); jasno je da mogu da igraju tako do iznemoglosti, tj taj niz moze biti proizvoljne duzine (pocevsi od 6); za 40:40 imamo:

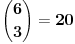
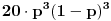
- niz sa 3 jedinice i 3 nule, dakle , sa verovatnocom za izjednacenje, ; naravno, da bi A pobedio, niz mora da se zavrsi sa 2 poena igraca A;

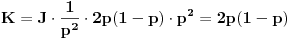
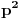
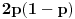
Neka je recimo J verovatnoca da se pobeda dogodila u j-tom pokusaju, a K da A dobija u j+2 pokusaju; to znaci da nije pobedio u j-tom, dakle skidamo dva keca sa prethodnog niza, dodajemo 01 ili 10 i na kraju 11; sto ce reci, . Ovo je znaci geometrijska progresija sa prvom clanom i kolicnikom , sto daje .

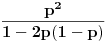
I tako bi konacni rezultat bio:

.

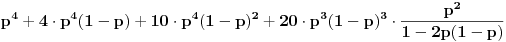
Rešenje je tačno. Ipak, vredi pomenuti da je ovo šablonski zadatak. Postoji postupak za rešavanje velikog broja srodnih zadataka.

Geometrijska raspodela?

Ovde se radi o lancima Markova.

Ako je događaj osvajanja gema od strane igrača A, znači prednost za igrača A, a prednost za igrača B, onda je verovatnoća osvajanja gema u odnosu na trenutni rezultat

,
,
.

Ovo je sistem od tri linearne jednačine sa tri nepoznate. Kada ga rešimo, možemo nastaviti dalje:

















je ono što je traženo. E, sad treba uraditi drugi zadatak.