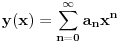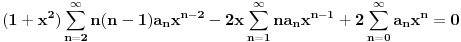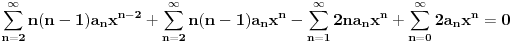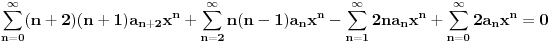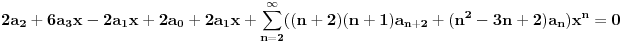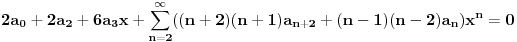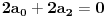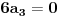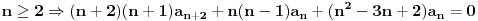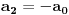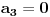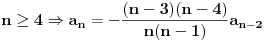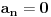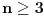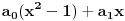Naći u obliku stepenog reda opšte rješenje DJ

[ kikik @ 22.10.2012. 11:59 ] @

Naći u obliku stepenog reda opšte rješenje diferencijalne jednačine

(1+x^2) y'' -2xy'+2y=0

http://speedy.sh/nYQEr/Zadatak.pdf

Jel može neko da mi pojasni malo..
Nije mi jasno kako se izračunavaju ovi koificijenti a2, a3, a4
Mislim da se u ovom prvom slučaju 2a2+3a0=0 .. 2a2 dobija tako što se gore na početku jednačine uvrsti n=2 u izraz n(n-1) an x^n-2, a ovo 3a0 tako što se na samom kraju uvrsti da je n=0 u 3an x^n ....
Ali ne znam zašto je to tako i ne znam za ove dalje kako dobija 3*2a3+5*1a1+3*a1=0..

Pozdrav

[ Nedeljko @ 22.10.2012. 13:39 ] @

Prvo, u pitanju je homogena linearna jednačina, koja se može lako rešiti po najvišem izvodu.

Osobina takvih jednačina je da njihova rešenja obrazuju vektorski prostor, čija je dimenzija jednaka redu jednačine, što sledi iz Pikarove teoreme o postojanju i jedinstvenosti rešenja. Dakle, ako nađemo dva linearno nezavisna rešenja bilo kojom metodom, završili smo posao. Potražićemo ga u vidu stepenog reda.