*

Jeste,ali kako si dosao do toga ?

Imaj u vidu da je logaritam manji od 1,a tada nije maksimum za sos(x)=1.
Nađi maksimum.

Znam to,al kako da nadjem maksimum ove funkcije :@ ima li neko ceo zadatak da uradi postupno :S

Dakle tebe muči kako izračunati ovo:

 

Znaš li zašto sam stavio -1 umjesto cos(x) i ono max ?

Ako neznaš pogledaj graf eksponencijalnih funkcija dole na dnu.(ubaciću to).

Sad imaš samo par koraka ovog tipa:

Umjesto log napravi eksponencijalni izraz iste jednačine.Nadam se da znaš kako se to radi ako znaš šta je to logaritam nekog broja.

-Rješi se onog minusa ovako:



Sad ponovo logaritmiraj obe strane (sa bazom log.koja ti paše,ali ne 10 ,e,2 ili nešto bog zna šta drugo).

Ako zalutaš javi gdje si stigao pa ćemo te uputiti u pravcu PMF.






_{[Ovu poruku je menjao zzzz dana 05.11.2012. u 18:23 GMT+1]}

Na grafiku treba da stoji a>1 i a<1, a ne od nule.

Možeš da uradiš zadatak i preko izvoda, jer se ovde maksimum poklapa sa najvećom vrednošću funkcije.

@mikio69 je u pravu.
Popravio.

Galaktikos Np se ne snalazi u ovome jer izgleda nezana ovakve stvari:



I ovo:

I ovo:

Ovo se teško pamti ako se nezna kako je nastalo.

A evo šta on hoće:

"Znam to,al kako da nadjem maksimum ove funkcije :@ ima li neko ceo zadatak da uradi postupno :S "


A to je u suprotnosti sa pravilnikom ovog foruma.Koliko ima smisla pokazati nekom kako se vozi auto,ako taj ne želi naučiti saobraćajne znake?

U postavci zadatka piše "...najveća vrednost funkcije...".
U sledećem komentaru autor zadatka to poistovećuje sa "...maksimum funkcije...".
Mislim da prvo treba da nauči da ta dva pojma nisu ista.
Posle da nauči sve ove "znake" koje je Milan napisao i nacrtao.

Najveća vrednost i maksimum jesu isto. Maksimalna vrednost je nešto drugo (mada u linearnim uređenjima isto što i maksimum), supremum nešto treće (ne mora se dostići, a ako se dostigne, onda je maksimum), a lokalni maksimum nešto četvrto (maksimum u bar jednoj okolini).

Ovaj jednostavni zadatak ima samo dva "postepena" koraka:

1)Uočiti maksimume ove dvije eksponencijalne funkcije.(prikazao sam na skici).
2)Izračunati te maksimume radi poređenja.

Ajmo pokušati.
Uzmem kalkulator i izračunam:


Takođe i

Tvrdim da ako 5 podignem na ovaj stepen dobiću 6.Kako sam ja to postigao kad na ovom comp Calculatoru nema logaritama sa bazom 5.Imamo samo prirodne i dekadske.

Ovako sam tipkao po kalkulatoru:(5),(log),(M+),(6),(log),(/),(MR),(=)
Ukupno 8 tipkanja.
Za M2 :(MC),(6),(log),(M+),(5),(log),(/),(MR),(=)(x^y),(1),(+/-),(=).
što je zapravo 13 tipkanja.
Ko zna kako se računaju logaritmi sa "divljom" bazom i zašto se baš tako računaju,odmah će mu biti jasno ( i bez ovog gore nepotrebnog izračunavanja)
koje od ponuđenih rješenja je ispravno.

Uslov je samo da se još zna i ovo

<sub>[Ovu poruku je menjao zzzz dana 21.11.2012. u 13:07 GMT+1]



[Ovu poruku je menjao zzzz dana 06.11.2012. u 13:10 GMT+1]</sub>

Ako je Miki069 u pravu kad kaze da se radi preko izvoda,onda mi je jasno sto ne razumem jer izvode ne znam,i jos ih nisam radio u skoli,ako se radi jednostavnije onda cu probat' nekako da skontam :) i pitam kako da izracunam maksimum ove funkcije,bez digitrona,i ne pametuj mnogo sa voznjom auta :)

Ja ne vidim razlog da se ovde petljaju izvodi.

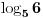
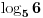
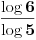
Prvo, ako imamo , sta primecujemo? Pa sad, sve zavisi od osobe do osobe, al da se primetiti da je ovde baza drugacija od standardne (recimo da za standardnu podrazumevamo kada je sa 10 ili ). I mi se osecamo nelagodno da radimo sa njom. Sta onda zelimo? Pa valjda da se se vratimo tamo gde umemo (kolko tolko efikasno) da radimo. Kako to uradimo, pa jednostavno, predstavimo kao (uzmi za bazu šta ti duša ište, 10 il ). Dobro, sta dalje znamo? 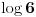Kakav je odnos izmedju i ?. 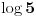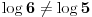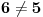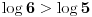Pa, mi znamo (trebalo bi) da je logaritamska funkcija rastuca funkcija, a kako je (jel jerbo znamo da je ) onda je , pa je i . 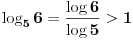I to nam je dovoljno za sada, da imamo predstavu (kakvu takvu) o kom broju se radi. 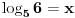Naravno, mogli smo da kazemo i , tj. 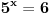, pa se da zakljuciti da je .

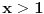
Mislim da sada nije tesko zakljuciti da je .

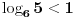
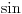
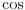
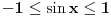
E sad, mi te brojeve "dizemo" na f-je odsnosno . Sta mi znamo o njima? Pa svakojake stvari, al za sada nam je bitno kakve one sve vrednosti mogu da postignu. Trebalo bi da nam je jasno da vazi i .

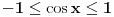
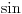
Pa sta? Pa nista, u prvom slucaju je u pitanju broj koji je veci od 1, pa kad on dostize max, pa sad, ako ga dizemo na negativni stepen onda ga u stvari smanjujemo, za nulu je jedan, a za stepen veci od nule ga povecavamo (sto neko rece, seti se kakva je eksponencijalna funkcija, al ja se ne bih gadjao sa takvim teskim terminima), pa dobro, koji je to najveci broj veci od nule koji moze da dostigne? Pa valjda 1, osim ako nesto nisam duvao. Stavis mu ti lepo jedan kao stepen, izracunas ti to lepo (ako uopste i ima sta da se racuna) i eto tebi tvog resenja za .

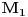
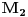
Drugi slucaj se posmatra slicno, sem sto sada imamo broj koji je veci od nule, manji od jedan, pa dobro, kod njega se stepenovanje ponasa suprotno od proslog primera, valjda ne treba nista koobjasnjavati, stavis ti lepo -1 kao stepen, on ga cap obrne i onda dobijes resenje za i da te vidi babo.

Može i preko izvoda, a ne mora.
Najprostije je kako ti je Sonec uradio.
Možda te oni bune što neće da ti kažu za koje X-eve se to događa:
M1 postiže najveću vrednost prvi put za X= pi/2 (90 stepeni) i ta vrednost iznosi LOG5(6).
M2 postiže najveću vrednost prvi put za X=pi (180 stepeni) i ta vrednost iznosi LOG5(6).


_{[Ovu poruku je menjao miki069 dana 07.11.2012. u 00:00 GMT+1]}

Ja sam Mikiju dao za pravo kad je primjetio da je na dijagramu umjesto a>1 stajalo pogrešno a>0.A za računanje maksimuma preko izvoda nije u pravu mada u principu može.(Nepotrebno dug posao i zahtjeva nešto napredniji nivo znanja).

Evo zašto ja pametujem sa vožnjom auta:
Želim da se podsjetiš na ono što si učio u 2-3 razredu srednje,a izgleda zaboravio.A ti umjesto toga tražiš kako to konkretno rješenje treba da izgleda.

Pa evo:





Sad si hepi,a ja prekrših pravilnik ovog foruma.Sad nalupetaj ovo napamet i trči položi prijemni.Nemoj se zamajavati sa glupostima zašto je i otkuda :



i smije li to biti naprimjer ovako sa prirodnim logaritmima?



Ja se potrudih da uputim kako ćeš sam doći do onog rješenja,ali izgleda da od tog nema ništa.Magare je magare.