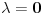
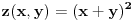
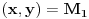
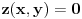
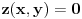
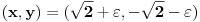
Za je Lagranževa funkcija upravo . Kada je , onda je . Možemo li u okolini te tačke naći tačke u kojima je vrednost Lagranževe funkcije negativna? Očigledno ne. Možemo li u okolini te tačke naći i druge tačke u kojima je ? Pa, možemo, za blisko nuli (ne mora biti pozitivno) i nikakve druge. Da li neka od tih tačaka zadovoljava uslov? Da vidimo:

,
,
,
,
,

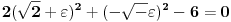
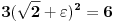
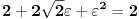
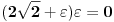
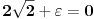
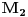
što ne može biti tačno za dovoljno blisko nuli. Dakle, imamo lokalni minimum u toj tački. Slučaj tačke je analogan. Postojanje lokalnog ekstremuma smo mogli utvrditi i tako što bismo rešili sistem diferencijala jednačine i uslova.

,
,

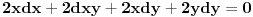
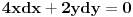
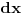
Delenjem obe jednačine sa dobijamo sistem od dve diferencijalne jednačine


.

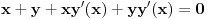
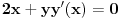
Tražimo im zajedničko rešenje, koje zadovoljava Košijev uslov vezan za tačku lokalnog ekstremuma .

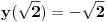
Oduzimanjem druge jednačine od prve dobijamo


.

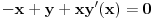
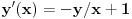
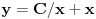
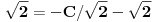
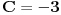
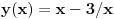
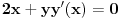
Ovo je linearna jednačina prvog reda, čije je opšte rešenje . Obzirom na Košijev zadatak, mora biti , tj. , pa je . Da li se to uklapa u jednačinu . Ne baš.

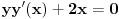
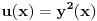
Naravno, lakše je bilo rešavati jednačinu (smenom i dobićemo tačno uslov iz postavke zadatka), ali sam hteo da pokažem da se te dve jednačine smeju sabirati/oduzimati ako je podesno.

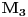
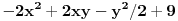
U tački Lagranževa funkcija glasi . Ispitajmo diferencijal Lagranževe funkcije pod uslovom da je diferencijal uslova jednak nuli i da smo blizu tačke koju razmatramo.

,
.

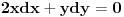
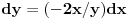
Zamenimo to u Lagranževoj funkciji

,

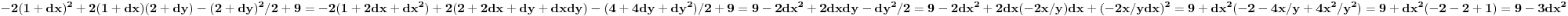
pa imamo lokalni minimum.

Što se oblasti tiče, treba ispitati stvar i na granici. Dakle,

,
.

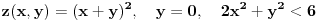
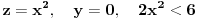
Jasno je da je ovde minimum tačka (0,0) i da drugih lokalnih ekstremuma nema.

Isto tako se analizira slučaj



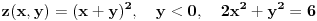
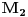
gde otpadaju tačke i .

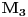
Kada radimo unutar oblasti, nemamo uslove, tj. onda se minimum dostiže na otvorenoj duži .

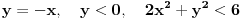
Naravno, ostale su nam i tačke .

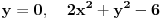
E, kad odrediš vrednosti funkcije u svim kritičnim tačkama (nevažno je da li među njima ima i viška), onda se najmanja i najveća vrednost dostižu u nekim od tih tačaka.