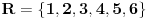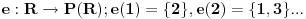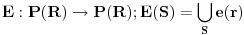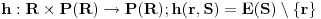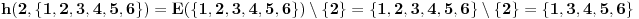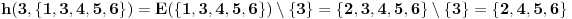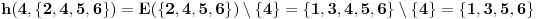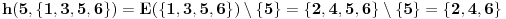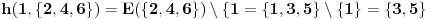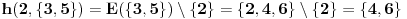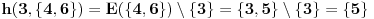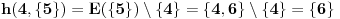Ideja:

proverim 1
ako nije, mogla je biti u 2, 3, 4 ili 5

proverim 2
ako nije, moguci su sledeci prelazi: 2->{1,3}, 3->4, 4->{3,5}, 5->4; dakle sada se nalazi u skupu {1,3,4,5}

proverim 3
ako nije, moguci su sledeci prelazi: 1->2, 3->{4,5}, 4->5, 5->4; skup mogucnosti je {2,4,5}

proverim 4
ako nije, moguci su sledeci prelazi: 2->{1,3}, 4->{3,5}, 5 nema gde; skup mogucnosti je {1,3,5}

proverim 2
ako nije, moguci su sledeci prelazi: 1 nema gde, 3->4, 5->4; skup mogucnosti je {4}

Znaci da bi posle svega, lisica morala biti u jazbini br 4.

Ako bih najpre proverio prvu rupu, onda bih u slučaju neuspeha znao da je u 2, 3, 4 ili 5, što znači da sledećeg jutra može biti u bilo kojoj od rupa, tj. nisam izveo nikakav zaključak. Dakle,

1 otpada (sve je moguće),
3 otpada (sve je moguće),
4 otpada (svodi se na isto kao za 2, pa nema potrebe razmatrati oba slučaja),
5 otpada (sve je moguće.

Proverim 2. Ako nije, moglo je biti 1, 3, 4, 5. Mogućnosti za sledeće jutro su 2, 3, 4, 5.

Sledeća provera:

2 otpada (vraćanje na isto),
4 otpada (posle se vraća ne simetričan slučaj sa 2, 3, 4, 5),
5 otpada (sve je moguće).

Proverim 3. Ako nije, moglo je biti 2, 4, 5. Mogućnosti za sledeće jutro su 1, 3, 4, 5.

Sledeća Provera:

1 otpada (vraćanje na 2, 3, 4, 5),
3 otpada (vraćanje na 2, 3, 4, 5),
5 otpada (sve je moguće).

Proverim 4. Ako nije, moglo je biti 1, 3, 5. Sledećeg jutra može biti 2, 4.

Sledeća provera:

4 otpada (svodi se na isto kao za 2, pa nema potrebe razmatrati oba slučaja).

Proverim 2. Ako nije, bilo je 4. Sledećeg jutra može biti 3, 5.

Sledeća provera:

5 otpada (vraćanje na 2, 4).

Proverim 3. Ako nije, onda je 5. Sledećeg jutra je 4.

Hvatam u 4.

Dakle, postoje dva optimalna rešenja: 2, 3, 4, 2, 3, 4 i 4, 3, 2, 4, 3, 2.

darkosos

Imaš dve greške. Prvo, provera prve rupe je bila nepotrebna, jer nisi dobio nikakvu novu informaciju, a kada si na kraju ustanovio da je u 4, ti si tog dana iskoristio jednu proveru i moraš čekati sledeće jutro, kada će biti u 3 ili 5.

Interesantno da je, ako nisam nigde pogresio, moje resenje takodje u 6 koraka (1,2,3,4,2,4), iako sam video kasnije da pocinjanje sa prvom rupom kao da ne donosi nista.

U tom smislu je i to resenje "optimalno", ako je rec o broju koraka u kojem se lisica hvata. Interesantno bi bilo pokusati naci opsti algoritam, posto Milan izaziva sa generalizovanim slucajem...

Nedeljko, nisam siguran za ovo drugo, u mojoj analizi "prelaz" znaci analizu onoga sto se desilo prethodne noci, pa ako sam ustanovio da je prethodne noci smugnula u 4, onda cu je tu i naci sledeceg dana.

Posle provere da nije u 2, zaključio si da je sada u 4, ali je nisi uhvatio. To što si zaključio u kojoj je jazbini ti ne daje za pravo da je uhvatiš ako si proveru tog dana već iskoristio. Sledećeg dana neće biti u 4, već u 3 ili 5.

Da, u pravu si, treba dodati jos proveru za 3, cime se lisica sabija u 5, odakle nema gde nego u 4. Dakle ako izbacim 1, dobijam tvoje resenje 234234. Ocigledno da vazi i simetrija, moze se krenuti sa drugog kraja.

Dakle, ako imamo n rupa, mozda bi dva resenja mogla biti 2,3,..,n-1,2,3,n-1 i isto to samo naopacke.

Ma bre, samo poranite jedno jutro i dodjite pre lisice i videcete gde se sakrila a onda bam-bam i gotovo

Pod uslovom da lisica nasumično bira sledeću rupu u kojoj će prespavati, verovatnoća da je pronađeš u bilo kojoj rupi bilo kada je 20 procenata :) Nije bitno koju rupu proveravaš, bitno je da to radiš dovoljan broj dana i (skoro) sigurno je hvataš :)

Samo što to nije ovaj zadatak.

Da još malo pojasnim ovaj problem:
1) Kad bi lisica nasumično birala jazbinu za povratak,tada bi klasičnom teorijom vjerovatnosti lako izračunali šansu (vjerovatnost) da je ukebamo u n pokušaja.Za bilo koji po volji odabrani broj jazbina.
2)Lisica ne bira rupu nasumično.Mora se vratiti u susjednu,lijevu ili desnu.
3)Ovo ograničenje za neke male brojeve jazbina osigurava 100% pogodak u ograničenom broju pokušaja da će biti ukebana.Naprimjer za 2 jazbine šansa da je iz prve uhvatimo je 0.5, a iz dva pokušaja 100%.Evo ga Nedeljko i Darko nađoše siguran put čak i za 5 jazbina.
4)Ima li siguran postupak za 6 ili još više jazbinajazbina?
5)Ako nema, da li ovakvo ponašanje lisice uvećava šansu u odnosu na slučaj opisan pod 1)?Po svoj prilici da.Da li se to matematički može izraziti a da ne koristimo montekarlo metode.?

Mislim da sam nasao resenje za 6: 2 3 4 5 2 3 4 2 3 4 5; da li je to najmanji broj koraka, ne znam. A mozda sam i zgresio nesto :)
U svakom slucaju pada u vodu ideja o prostom nastavljanju uocene logike na primeru sa 5 rupa. Mada i ovde ima neke pravilnosti.
Izgleda da je kljucno da se lisica sabije u isti skup mogucnosti, jer sa nadalje ponasa isto bez obzira na izbor rupe.
Aj' okacicu i slidzu, mada sam je vec ispravljao ses' puta, i vise me mrzi, moguce je da sam opet oman'o.

Skinuo sam sliku odozgo, jer sam, kao sto sam obecao, oman'o.

Elem, evo nesto (citate na sopstvenu odgovornost):

Neka je dat skup i neka je P(R) njegov partitivni skup.

Definisemo sledece funkcije:






I onda mozemo ovako da igramo:

Bravo darkosos, rešenje 234512345 je tačno.

Na prvu mi se čini da opšta strategija zavisi samo od toga da li je broj jazbina paran ili neparan.
Za n=5 ide 2-3-4-2-3-4. Svaka jazbina je jednom prolazu prođe na parnom (neparnom) a sledećem krugu na neparnom (parnom) mestu.
Za n=6 ne pije vodu 2-3-4-5-2-3-4-5 jer bi svaka jazbina u oba ciklusa bila pretražena u istoj parnosti. Mora između ciklusa da se ubaci jedan dan "pauze" da
se promeni parnost, pa ide 2-3-4-5-1-2-3-4-5. Milsim da 1 nije morao ni da obilazi, već je mogao da uzme slobodan dan.

Nisam se udubljivao ali mislim da je za n=7 rešenje: 2-3-4-5-6-2-3-4-5-6.
Za n=8: 2-3-4-5-6-7-1-2-3-4-5-6-7.

Uopšteno za neparne n: 2-3-4...-(n-1)-2-3-4...-(n-1), a
za parne n: 2-3-4...(n-1)-pauza-2-3-4...-(n-1).

Imam pametnijih poslova, a ne da trazim jazbine i lisice... ;S

Čudo da si uopšte na forumu i da još odgovaraš pored toiko pametnijih poslova.

@miki069

Mislim da si u pravu za taj dan pauze, cak i ako ne odbacim 1 u petom pokusaju, ostalo bi {1,3,5}, koje se pretvara u {2,4,6} i dalje isto. U principu, da bi se ostalo u kontekstu zadatka, moze da se koristiti 1. Verovatno se moze pokazati da se u opstem slucaju posle prvog prolaza dobija niz 2,4,6,... za paran broj rupa i 1,3,5,... za neparan broj rupa. Takodje, tacno je da se cekanjem jednog dana u prvom slucaju, dobija neparan niz 1,3,5,... Valjalo bi jos samo pokazati zasto ovaj niz sada nestaje biranjem redom 2,3,4,... U stvari znam :) Ovakav niz svakako svakim narednim danom menja parnost, a trazenjem redom u 2,3,4, polako se "jede" jedna po jedna rupa.

Ovaj zadatak je iz nekih ruskih izvora.Navodno,vezan je za teoriju kvantne mehanike.Nisam znao rješenje,ali ovaj pokušaj od @miki069 je odlična polazna osnova.

Hajdemo ovako:

-Neka imamo n jazbina.Pokušajmo pronaći lisicu u prvoj.Ako je nema onda je lisica spavala u jazbini udaljenoj za 2k ili 2k-1 mjesta.

-Ako je bio prvi slučaj tjerajmo polako 2,3 itd sve do n-1.Nema šanse da se paran razmak poremeti,tj lisica ne može preskočiti nazad.

-Ako je ni u n-1 jazbini nema onda je možda preskočila nazad ili je upravo u n-toj jazbini.(Početni razmak j bio 2k-1)

-Provjerimo još jednom n-1 jazbinu.(Time ujedno
neparan razmak pretvorimo u paran.)

-Ako je ni tada nema onda hajdemo polagano provjeravati unazad n-2,n-3,...nema šanse da preskoči.

Ovom strategijom sigurno hvatamo lisicu za 2n-3 dana.Može li brže?

Milane, bilo bi zanimljivo da napises tu vezu sa kvantnom mehanikom. Da ne ispadne da stvarno samo jurimo lisicu :) Naravno, zadatak je zanimljiv i samo sa matematicke strane.

Drugo, mislim da nema potrebe da proveravas 1, vidi prvu Nedeljkovu poruku. Ne samo to. nego je tada po tvojoj taktici broj trazenja 2n-2 ( = 1+n-1+1+n-3). Naravno ako je u 1 i odmah je nadjes, mozes da platis pivo kafani, ali to vazi za svaku rupu.

Sem toga, postupak izgleda dobro, kao i onaj koji je prikazao miki069. S tim sto nema potrebe za ponavljanjem n-1 ako je broj rupa neparan, pokazali smo vec da je za n=5 dovoljno 6 provera (2n-4). Dakle to bi sve zajedno znacilo 2n-3 provera za parno n i 2n-4 ( = 2(n-2)) provera za n neparno.

S drugu strane, jedino je Nedeljko razmatrao optimalnost resenja, ja sam samo pokusavao da resim kakogod, koristeci pre svega intuiciju :) I dalje mi nije jasno zasto dobijam razredjen skup posle prvog prolaza (odnosno 1,3,5,... ili 2,4,6...) ali mi je jasno sta treba posle da radim...

OK.Ne treba poći od prve rupe već od druge.Bez obzira na broj jazbina tada može maksimalno biti 2n-4 provjera.Ponavljanje n-1 rupe je korisno jer tada nije važno da li je njihov ukupni broj paran ili neparan.A na kraju ne moramo tjerati do 1.Posao je gotov u najgorem slučaju kod 2. (Zato je ono moje bilo 2n-3 koje sada ispravljam na 2n-4)

Dakle za n jazbina treba provjere vršiti ovako;

2,3,4,.......,i,i+1,........,n-1,n-1,n-2,n-3,..,i,i-1,....4,3,2.
-------------------------------- ---------------
-------------------------------- ---------------
Za kvantnu mehaniku nisam baš neki stručnjak,ali valjda se misli na nešto ovako:

Elementarne čestice, na mikrokozmičkom nivou se ne daju odrediti deterministički. Apsolutna sigurnost stanja (položaja) nije odrediva; moguć ih je jedino opisati zakonima vjerojatnosti. Ovo je poznato kao Heisenberg-ov princip neizvjesnosti.
Naprimjer elektroni preskaču između susjednih elektronskih ljuski nepredviđeno,nešto kao i ova lisica.
Ako još nešto saznam o vezi ovog zadatka i K. T. javiću.