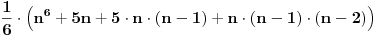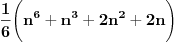[ Sonec @ 12.11.2012. 11:17 ] @
|
[ darkosos @ 13.11.2012. 20:27 ] @
Dal' moze ovako prvi:
- oznacimo temena sestougla brojevima 1 do 6, recimo u smeru kazaljke na satu - napravimo korespodenciju izmedju varijacija sa ponavljanjem n elemenata i temena, tako sto redom boje te varijacije dodelimo temenima sestougla. Time dobijamo sva moguca bojenja temena, kojih ima 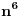 pa treba oduzeti koje su fiksne u odnosu ne neku rotaciju. Naravno, mogucih rotacija ima 6 i sto se tice varijacija, mozemo ih gledati kao ciklicno pomeranje boja. pa treba oduzeti koje su fiksne u odnosu ne neku rotaciju. Naravno, mogucih rotacija ima 6 i sto se tice varijacija, mozemo ih gledati kao ciklicno pomeranje boja.Razmotrimo koja su to bojenja invarijantna na te rotacije. Ako oznacimo jedno bojenje sa abcdef, onda ove rotacije znace sledece jednakosti boje: 1. rotacija za jedno mesto (a,b,c,d,e,f) -> (f,a,b,c,d,e), daje a=b=c=d=e=f 2. rotacija za dva mesta (a,b,c,d,e,f) -> (e,f,a,b,c,d), daje a=c=e i b=d=f (ova bi zahtevala da je n bar 2) 3. rotacija za tri mesta (a,b,c,d,e,f) -> (d,e,f,a,b,c), daje a=d, b=e i c=f (ova bi zahtevala da je n bar 3). Rotacija za 4 mesta ce dati isto sto i rotacija za 2, a za 5 mesta isto sto i ona za 1. Dakle, imamo 3 klase bojenja koje su invarijantne u odnosu na rotacije. Prva pomenuta klasa ima  elemenata. U drugoj kao da biramo 2 razlicite boje od n i da ih mozemo postaviti na 2 razlicita nacina, sto bi trebalo da je elemenata. U drugoj kao da biramo 2 razlicite boje od n i da ih mozemo postaviti na 2 razlicita nacina, sto bi trebalo da je 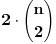 . Slicno, treca ima . Slicno, treca ima 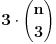 elemenata. Dakle, sve u svemu, to bi bilo elemenata. Dakle, sve u svemu, to bi bilo 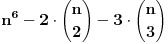 (u slucaju da je (u slucaju da je 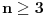 ). ).[ darkosos @ 16.11.2012. 11:13 ] @
[ Sonec @ 16.11.2012. 15:01 ] @
[ darkosos @ 16.11.2012. 22:58 ] @
Imas pravo, mogao sam da sredim, ali sam toliko sredjivao da bih dosao dovde, da mi je izgledalo veoma sredjeno :) Uostalom, sto samo ja da se mucim? :)
Elem, ja stvarno ne znam da li ovde ima zainteresovanih da vide izvodjenje, pa ne znam koliko ima smisla da to prezentiram? Mada sam kao rekao da cu napisati... Pa, ako neko procita od pocetka do kraja, nek' mahne u mom pravcu, da znam da je bilo i takvih. Kao sto rekoh, radi se o klasama ekvivalencije relacije "b nastaje rotacijom od a" u skupu varijacija n elemenata na 6 mesta, sa ponavljanjem. Nisam to bas tako tvrdo radio, ali to jeste apstrakt koji sam koristio. U grubo, postoje neke varijacije u kojima svih 6 rotacija (racunajuci i identitet) predstavljaju razlicite varijacije ("regularne"), i cine jedan skup klasa ciji broj elemenata treba deliti sa 6. One druge, koje sam vec ranije analizirao, stvaraju manje razlicitih varijacija. Evo sada opisa tih "neregularnih" varijacija, bez ulazenja potpuno u detalje: - oblik "aaaaaa" ima samo jedan element u klasi, a takvih klasa ima n; dakle ukupno n varijacija; ako imamo bar 2 elementa, 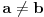 : :- oblik "ababab" ima 2 elementa u klasi, a klasa ima 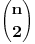 ; ukupno ; ukupno 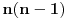 varijacija; varijacija;- oblik "aabaab" ima 3 elementa u klasi, a klasa ima 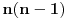 ; ukupno ; ukupno 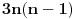 varijacija; varijacija;ako imamo bar 3 razlicita elementa, 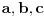 : :- oblik "abcabc" ima 3 elementa u klasi, a klasa ima 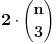 ; ukupno ; ukupno 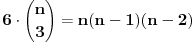 varijacija; varijacija;Naravno, svih varijacija ima 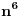 a broj regularnih dobijamo kao razliku ukupnog broja varijacija i broja neregularnih. Ovaj broj se deli sa 6, sto je zapravo zajednicki broj elemenata po klasi, i konacno treba dodati broj neregularnih klasa: a broj regularnih dobijamo kao razliku ukupnog broja varijacija i broja neregularnih. Ovaj broj se deli sa 6, sto je zapravo zajednicki broj elemenata po klasi, i konacno treba dodati broj neregularnih klasa: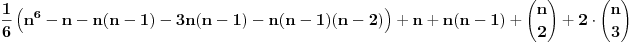 sto posle sredjivanja daje formulu koju sam naveo. sto posle sredjivanja daje formulu koju sam naveo.Interesantno je da formula "radi" i za n=1 i za n=2. [ Sonec @ 24.01.2013. 16:07 ] @
Nema razloga da ja previse tupim, kad postoji lepo ispisano resenje. Naime, ova dva zadatka su sa vezbi iz predmeta Algebre 2 i mogu se naci (uradjeni) OVDE (zadaci 36. i 37.)
Meni je bilo interesantno, pa sam zato postavio, a Darko je demonstrirao i drugaciji nacin resavanja problema. Zanimljivo, pricu oko [url=http://www.artofproblemsolving.com/Wiki/index.php/Burnside's_Lemma]Bernsajdova_lema[/url] se moze naci i u zbirci "Kombinatorika" Pavla Mladenovica. I zasto ne radi linkovanje u drugom slucaju? [ darkosos @ 25.01.2013. 08:00 ] @
U je, da li sam ja uopste polozio taj predmet? :) Iako je analiza manje vise slicna kao ono sto sam ja radio, sam racun je drugaciji, a ovo moje resenje je kao sto bi uradio neki spretniji srednjoskolac :)
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|