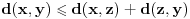[ miki069 @ 13.11.2012. 19:07 ] @
| Da ne kucam evo link do ispitnog roka: http://imi.pmf.kg.ac.rs/moodle...vni_kolokvijumi-06.02.2012.pdf Radi se o prvom zadatku sa prvog kolokvijuma. Interesantan je, jer pokazuje da od četiri aksime metričkog prostora su dve suvišne kao aksiome: 1. nenegativnost d(x,y)>=0 i 2. simetričnost d(x,y) = d(y,x), jer su posledica ostale dve aksiome navedene u ovom zadatku. Nigde ovo ranije nisam sreo kao neku teoremu, a malo mi glupo da od četiri aksiome, dve kao kao i nisu aksiome. Prvo sam mislio da je neispravan zadatak i bezuspešno sam tražio kontra-primer. Međutim, zadatak je ispravan i uradio sam ga. Ako nekom treba otkucaću rešenje. [Ovu poruku je menjao miki069 dana 13.11.2012. u 23:07 GMT+1] |