Mozda da probas indukcijom... Recimo da se primeti da je . Indukcija bi onda bila preko prethodna dva, sto nije problem, posto imas da vazi za n=1 i n=2. Samo treba obratiti paznju da iako po pretpostavci i ne bi bili deljivi sa 5, ne mora da znaci da njihova razlika nije deljiva sa 5, ali mislim da to moze da se raspetlja,

Ja bih jednostavno rešio kvadratnu jednačinu , a onda bih napisao šta je tačno .

,

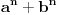
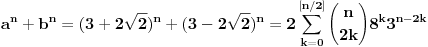
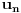
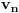
odakle sledi da jeste u pitanju ceo broj. Ovo je ništa drugo do ceo broj takav da za odgovarajući ceo broj važi .

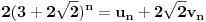
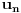
Dakle, mi treba da dokažemo da nije deljivo sa 5. Iz



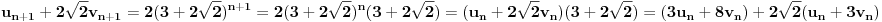
zaključujemo da je

, .

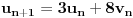
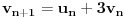
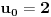
Pritom je i .

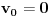
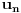
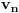
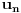
Odavde se lako indukcijom dokazuje da se ostaci pri delenju brojeva i sa 5 javljaju periodično sa periodom 6, oodakle nije teško zaključiti da nije deljivo sa 5 ni za jedno .

_{[Ovu poruku je menjao Nedeljko dana 17.11.2012. u 14:22 GMT+1]}

Bravo, Darko. Obzirom da su i poznati, to se svodi na

.

Znači, ostaci su

2, 1, 4, 3, 4, 1,...

a onda se periodično ponavljaju.

E vidis, moze i tako... Video sam tu jednakost po modulu 5, ali sam pomislio da i to moze da se ugura u indukciju, posto nikoja 2 uzastopna izraza ne mogu dati isti ostatak posle deljenja sa 5, pod pretpostavkom da nijedan nije deljiv sa 5.

_{[Ovu poruku je menjao darkosos dana 17.11.2012. u 14:54 GMT+1]}

Hvala puno obojici na trudu i brzini.

Darkovo rešenje mi se malo više sviđa :)

A kome se ne bi vise svidelo krace i elegantnije resenje?