Pođi od definicije izvoda. Šta je ?

pa trebalo bi da je prvi izvod. Ali kako konkretno to ovde primeniti ?

Sad treba dokazati da kada prvi sabirak teži , drugi nuli, a treći . Naravno, sve to važi pod određenim uslovima za funkcije i .

treba da buse samo neprekidno. treba da bude definisano i neprekidno na ako je , odnosno na ako je , odnosno na ako je i da na tom pravougaoniku postoji i bude neprekidan parcijalni izvod od po .

Svi uslovi koje si naveo su zadovoljeni po pretpostavci teoreme čijeg je ovo deo dokaza. Jedino mi u njenom dokazu nije bio jasan korak koji sam naveo još u prvoj poruci. Hvala za uloženi trud, mada verujem da postoji neki očigledniji način, pošto na predavanjima nije posvećena posebna pažnja tome ( a obično se sve postupno radi )

Tako se radi, a postoji opsta formula za izvod po od . Zato se tome ne pridaje paznja.

Ajde kad si se već setio te formule, podseti i mene

Probaj da je izvedeš na prethodno opisani način.

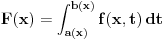
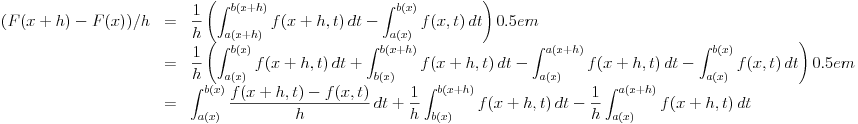
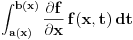
Kada prvi sabirak teži ka ako je parcijalni izvod funkcije po prvoj promenljivoj definisan i neprekidan na skupu .

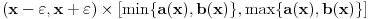
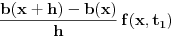
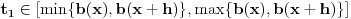
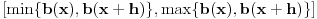
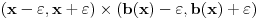
Drugi sabirak je po prvoj teoremi o srednjoj vrednosti za integrale jednak za neko ako je funkcija neprekidna po drugoj promenljivoj na , a ukoliko je funkcija neprekidna na i funkcija je diferencijabilna u , onda drugi sabirak teži ka .

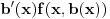
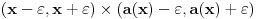
Ako je pritom funkcija neprekidna na i funkcija ima izvod u , onda na sličan način umanjilac teži ka .

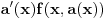
Dakle, ako su ispunjeni uslovi

1) parcijalni izvod funkcije po prvoj promenljivoj je definisan i neprekidan na skupu ,

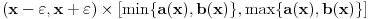
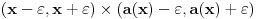
2) funkcija je neprekidna na i ,

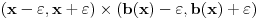
3) funkcije i su diferencijabilne u tački ,

onda je

.

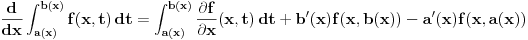
To je nista drugo do Leibniz-ovog pravila za diferenciranje ispod znaka integrala. Pogledati prilog.

Tja, mogao si da okačiš to ranije da ne moram ja da kucam. Džaba sad.

Da si napisao kako izgleda konacna formula kad si bio pitan onda bih i okacio (jer sam smetnuo sa uma ovo pravilo, a da si ga napisao setio bih ga se momentalno). Mislim da nije bas sad dzaba, bar zna kako se zove pravilo (ako se nekada bude pozivao na njega), a i ovo moje ima i malo price oko samoga stava (oko pomocnih stavova koji se koriste u dokazu, na primer).