[ bags @ 07.03.2004. 18:57 ] @
|
| Moze li mi neko pomoći oko ovog zadatka :
Pokazati pomoći matematičke indukcije ,da za rekurzivno definisanu funkciju :
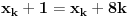 za svako k =>1 za svako k =>1
važi 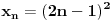 za svako n => 1 . za svako n => 1 .
Zadatke kada su dati nizovi preko opšteg člana znam riješavati,ali ovo mi je prvi ovakav ,a nemam primera ni u skripti ni u knjizi,pa ako bi neko mogao da da smjernice bio bih zahvalan.
|
[ noviKorisnik @ 07.03.2004. 21:44 ] @
Fali ti početni uslov, koliko je x1?
Pošto se traži dokaz putem indukcije, verovatno nije predviđeno da dođe do pucanja pri prvom koraku, tako da bih rekao da je x1 = 1.
Sada klasična indukcija:
Korak 1: k=1:
x1 + 1 = x1 + 8*1
x2 = 1 + 8 = 9
proverimo da li zadovoljava: x2 = (2*2 - 1)2 = 9. OK
Korak 2: pretpostavka: za k = n-1 važi
xn = xn - 1 + 8(n - 1) = (2n - 1)2
Korak 3: k = n
Znamo: xn + 1 = xn + 8n
Treba pokazati: xn + 1 = (2(n + 1) - 1)2
... to pokušaj već sam. Zadatak se i svodi na to da dokažeš da zadani rekurzivni oblik člana niza ima opšti član jednak drugom izrazu.
[ bags @ 09.03.2004. 13:38 ] @
Hvala što si napisao fino cijeli postupak.
Dalje je bilo stvarno lako. :)
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.