Tom metodom ne može.

Inace, ta metoda je poznata pod nazivom Kramerovo pravilo.

A kojom inače može ?

Uvedeš smenu , , pa onda imaš sistem

,
,
,
,
.

Prve tri jednačine su linearne. Rešiš njih i ako su nezavisne, dobićeš rešenje koje zavisi od dva parametra, na primer i . Recimo da je

,
,
,
.

Zamenimo to u poslednje dve jednačine.

,
.

Ovo je sistem od dve kvadratne jednačine sa dve nepoznate. Iz prve možeš da izraziš preko , s tim da ćeš imati neki koren. To zameni u drugoj jednačini i dobićeš jednačinu samo po . Onda prebaci koren na jenu stranu, a sve ostalo na drugu, pa kvadriraj tu jednačinu da bi se oslobodio korena. Dobićeš jednačinu četvrtog stepena po . Postoje Feraraove formule za rešavanje jednačine četvrtog stepena, pa reši nju. Kada nađeš rešenja, onda izrazi preko . Obavezno proveri šta su od toga zaista rešenja i na kraju vrati sve to u izraze za , i i to ti je to. Treba da u opštem slučaju dobiješ četiri rešenja.

Kako se određuju tu vrednosti alfa1, beta1, ..., p, q, kako se zove ta metoda ? I da li je to jedini način ?

Npr. kako bi se rešio ovaj primer postupno


_{[Ovu poruku je menjao Nikola 23 dana 09.12.2012. u 15:37 GMT+1]}

,
,
,
,
.

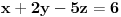
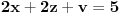
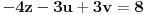
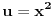
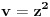
Oduzimanjem prve jednačine pomnožene sa 2 od druge se dobija

,
,
.

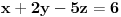
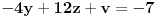
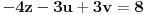
Delenjem druge jednačine sa -4 dobija se

,
,
.

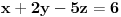
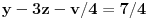
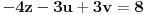
Oduzimanjem druge jednačine pomnožene sa 2 od prve dobija se

,
,
.

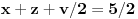
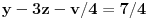
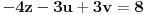
Delenjem treće jednačine sa -4 dobija se

,
,
.

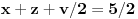
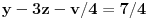
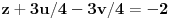
Dodavanjem treće jednačine pomnožene sa 3 drugoj dobijamo da je

,
,
.

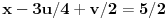
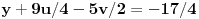
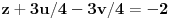
Preostale dve promenljive možemo uzeti za parametre, tj.

,
,
.

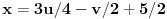
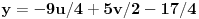
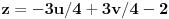
Sada to treba zameniti u poslednje dve jednačine

(*) ,
(*') .

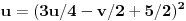
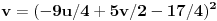
Posle sređivanja prve jednačine dobijamo

,

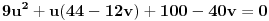
odnosno

.

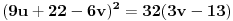
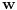
Uvedimo novu promenljivu sa

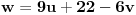
, odnosno .

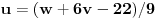
Prethodna jednačina postaje

.

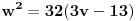
Jednačina (*') se može zapisati kao

.

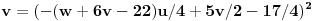
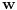
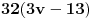
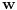
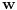
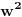
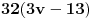
Posle kvadriranja zameni sa . Dobićeš jednačinu po i . Prebaci na jednu stranu, a sve ostalo na drugu. Kvadriraj jednačinu i ponovo zameni sa . Dobićeš jednačinu četvrtog stepena po . E, onda nju treba da rešiš, pa da se vratiš natrag kroz smene.