Ne bi bilo loše da se zna šta je X(s).

x(s). Odatle ooperator uzima vrijednost...

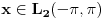
Ovo je ništa drugo do ta parcijalna suma Furijeovog razvoja -periodične funkcije pomnožena sa 2, a to je ograničen operator.

,
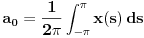
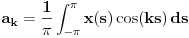
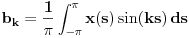
, za .

,

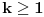
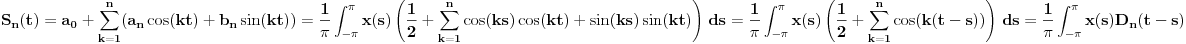
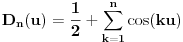
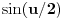
gde je Dirihleovo jezgro. Množenjem i delenjem Dirihleovog jezgra sa dobijamo da je

.

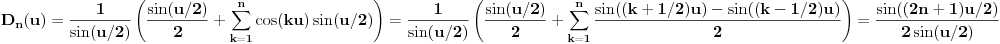
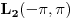
E, sad, -ta parcijalna suma Furijeovog reda je zapravo projekcija na potprostor generisan funkcijama , a projekcijski operator na potprostor dimenzije bar 1 uvek ima normu 1. Naravno, u normi razmatranog Hilbertovoh prostora, a to je kod tebe u njegovoj uobičajenoj normi, što ti se i traži.

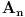
Dakle, za svako operator ima normu 2.

EDIT: Ispravka grešaka u kucanju.

_{[Ovu poruku je menjao Nedeljko dana 11.12.2012. u 12:13 GMT+1]}

Svaka vam cast...Ni priblizna mi nije bila ideja...A mislio sam citav sat o ovome...