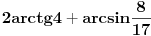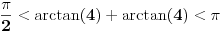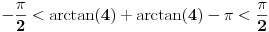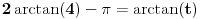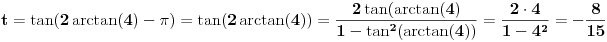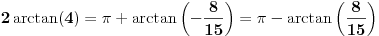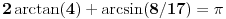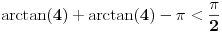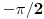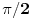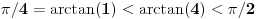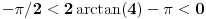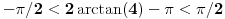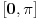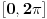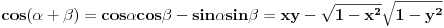[ nePonovljivA @ 11.12.2012. 22:47 ] @
|
[ Nedeljko @ 11.12.2012. 23:10 ] @
Ako je
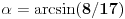 , koliko je , koliko je 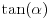 ? Pa, prvo je ? Pa, prvo je 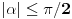 i i 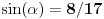 na osnovu definicije arkussinusa. No, onda možemo zaključiti da je na osnovu definicije arkussinusa. No, onda možemo zaključiti da je 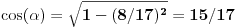 , pa je , pa je 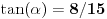 . Odatle i iz . Odatle i iz 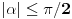 sledi da je sledi da je 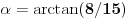 . Dakle, tebe zanima koliko je . Dakle, tebe zanima koliko je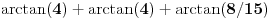 . .Neka je 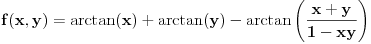 . .Obziom da je 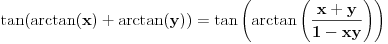 funkcija  sve tačke za koje je definisana slika u celobrojne umnoške broja sve tačke za koje je definisana slika u celobrojne umnoške broja  . No, domen joj se sastoji iz tri oblasti: . No, domen joj se sastoji iz tri oblasti: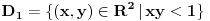 , ,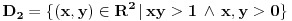 , ,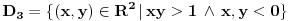 . .Obzirom da je funkcija  neprekidna, neprekidna slika povezanog skupa je povezan, a kodomen funkcije je potpuno nepovezan, ona je na svakoj od oblasti konstantna. Nije teško videti da se neprekidna, neprekidna slika povezanog skupa je povezan, a kodomen funkcije je potpuno nepovezan, ona je na svakoj od oblasti konstantna. Nije teško videti da se 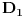 slika u nulu (jer se tačka slika u nulu (jer se tačka 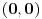 slika u nulu), slika u nulu), 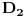 u u  (npr. na osnovu limesa kada (npr. na osnovu limesa kada  ), a ), a 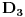 u u 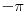 (na osnovu limesa kada (na osnovu limesa kada 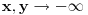 ). ).Stoga je 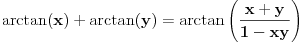 za za 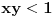 , ,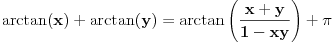 za za 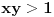 i i 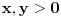 , ,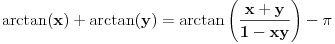 za za 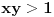 i i 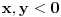 , ,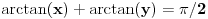 za za 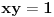 i i 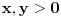 , ,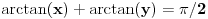 za za 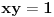 i i 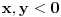 . .Poslednje dve relacije slede otuda što su tangensi oštrih uglova koji se dopunjuju do pravog recipročni i neparnosti tangensa. Dakle, 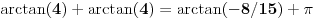 , ,pa je ceo zbir jednak  . .[ nePonovljivA @ 12.12.2012. 21:40 ] @
Zahvaljujem na trudu i vremenu
Imam još jednu nedoumicu: Za x i y iz [-1,1] treba dokazati da je  (dva slučaja su, ali ne umem da otkucam zagradu da bude velika Ako je 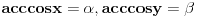 i i 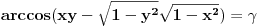 tada dobijam prvi slučaj na osnovu formule za tada dobijam prvi slučaj na osnovu formule za 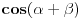 i osnovne trigonometrijske jednakosti primenjene na i osnovne trigonometrijske jednakosti primenjene na  i na i na  . Treba mi pomoć oko toga gde da primenim data ograničenja za x+y i kako da dobijem slučaj dva. . Treba mi pomoć oko toga gde da primenim data ograničenja za x+y i kako da dobijem slučaj dva.[ Nedeljko @ 12.12.2012. 22:39 ] @
[ nePonovljivA @ 13.12.2012. 00:19 ] @
[ Nedeljko @ 13.12.2012. 01:44 ] @
[ nePonovljivA @ 14.12.2012. 09:05 ] @
e sada je jasno.
Hvala puno. Jel znaš odgovor na ovo Citat: nePonovljivA: Za x i y iz [-1,1] treba dokazati da je  (dva slučaja su, ali ne umem da otkucam zagradu da bude velika Ako je 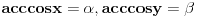 i i 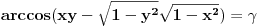 tada dobijam prvi slučaj na osnovu formule za tada dobijam prvi slučaj na osnovu formule za 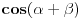 i osnovne trigonometrijske jednakosti primenjene na i osnovne trigonometrijske jednakosti primenjene na  i na i na  . Treba mi pomoć oko toga gde da primenim data ograničenja za x+y i kako da dobijem slučaj dva. . Treba mi pomoć oko toga gde da primenim data ograničenja za x+y i kako da dobijem slučaj dva.[ Nedeljko @ 14.12.2012. 16:40 ] @
[ nePonovljivA @ 14.12.2012. 19:17 ] @
[ Nedeljko @ 14.12.2012. 20:09 ] @
Neka je na primer
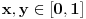 . U tom slučaju je . U tom slučaju je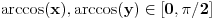 , ,pa je 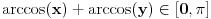 , a to je , a to je 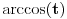 za neko za neko  . .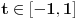 se lako određuje iz uslova se lako određuje iz uslova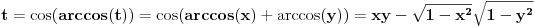 . .Znači, 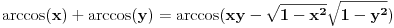 . .Neka je sada 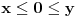 i i 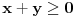 . To znači da je . To znači da je 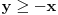 i i 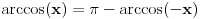 , odakle je , odakle je 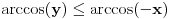 , pa je , pa je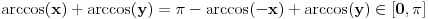 , a to je , a to je 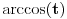 za neko za neko 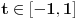 . Stoga je . Stoga je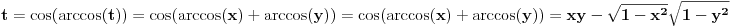 jer zbog 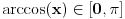 važi važi 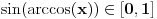 , odnosno , odnosno 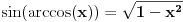 . .E, sad probaj da izvedeš reostale slučajeve. Edit: Ispravka greške. [Ovu poruku je menjao Nedeljko dana 15.12.2012. u 12:01 GMT+1] Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|