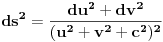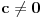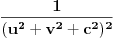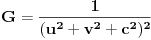[ markkooo @ 16.12.2012. 16:59 ] @
|
[ Sonec @ 16.12.2012. 18:14 ] @
Na Wikipediji se moze naci jedna formula (sa kojom ja nisam familijaran) za racunanje Gausove krivine preko koeficijenata prve forme kada je
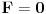 . .Ona kaze da je 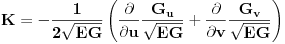 , koja se dodatno olaksava s obzirom da je kod nas , koja se dodatno olaksava s obzirom da je kod nas 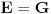 . Takodje, s obzirom na sam oblik . Takodje, s obzirom na sam oblik  , odnosno , odnosno  , kada se izracuna npr. , kada se izracuna npr. 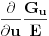 , lako se (s obzirom da su , lako se (s obzirom da su  i i  simetricno rasporedjeni) vidi sta je simetricno rasporedjeni) vidi sta je 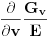 . Sve u svemu, posle ne tako dugog racuna dobija se da je (ako sam dobro izracunao) Gausova krivina . Sve u svemu, posle ne tako dugog racuna dobija se da je (ako sam dobro izracunao) Gausova krivina 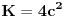 sto je konstatno naravno. sto je konstatno naravno.[ markkooo @ 16.12.2012. 18:47 ] @
Ok...hvala...sad cu racunati pomocu te formule...Nisam znao za tu formulu...Ja sam koristtio uopstene formule za Kristofijelove kkoef.
Pa sam za svaki koef.racunao i dobijao neki izraz... sve u svemu hvala puno... [ Sonec @ 16.12.2012. 18:54 ] @
Formulu mozes naci ovde: http://en.wikipedia.org/wiki/G...curvature#Alternative_Formulas
Pa eto, nisam ni ja znao. Ti si radio pretpostavljam preko Gausove Egregium teoreme, mogu misliti koliko si se namucio :) [ markkooo @ 16.12.2012. 19:08 ] @
Jesam jesam...kad nisam poludio....
Ma vjerovatno sam pogrijesio...a i ne pogrijesio koliki je racun...dvije dvolisnice... Dobio sam i zuljeve na prstima.... Hvala jos jednom... [ Sonec @ 16.12.2012. 20:49 ] @
Mislim (jer je nama profesor zapisao u drugacijem obliku) da jeste. Naime, mi smo ucili:
Teorema [Egregium, Gaus]. Neka je  regularna povrs u regularna povrs u 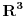 . Tada vazi: . Tada vazi: 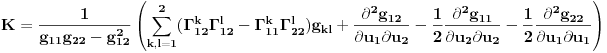 (gde su sa (gde su sa 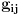 obelezeni koeficijenti prve fundamentalne formule i obelezeni koeficijenti prve fundamentalne formule i 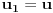 i i 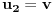 ) )I verovatno ako se jos iskoristi (unatraske) sledeca teorema se moze doci do te formule sa wikipedije: Teorema. Neka je  regularna povrs u regularna povrs u 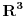 . Tada vazi: . Tada vazi: 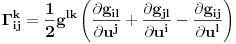 , gde je , gde je 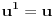 i i 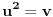 , a , a 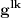 , huh, , huh, 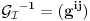 , gde je , gde je 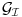 matrica prve fundamentalne forme. matrica prve fundamentalne forme.[ markkooo @ 16.12.2012. 20:56 ] @
Da to je egregium formula koju sam koristio....Koja koristi sako koeficijente prve fundamentalne forme...
Ja sam nasao u knjizi Janjica (Krive i povrsi) u nesto pogodnijem obliku od ovih...Ako kog zanima kakav je oblik mogu mu ispisati... (inace preko izvoda po u i v od F,G,E ) Pa sam ih kao takve i racunao... Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|