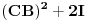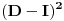Ono što si nazvala rezultatom svođenja je ok, ali zadnja formula koju navodiš nije.
Nakon tog koraka svođenja moraš celu jednačinu pomnožiti sa inverznom matricom od .
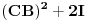
Vodi računa i o tome s koje strane množiš, jer množenje matrica nije komutativno u opštem slučaju.

Ako je bio lapsus u pitanju, pa je umesto invertovanja napisano X, onda je formula dobra.

Hvala vam puno.. Fraktal, u pravu si, jasno mi je da se mora voditi računa oko toga sa koje strane mnozim matricu, ali sam ja napravila gresku dok sam kucala: ( (CB)^2 + 2I)^-1 ovo mi je ta inverzna matrica, zaboravila sam da napisem i -1. To je ovaj krajnji zapis: X = ( (CB)^2 + 2I)^-1 * ( ACB - (D-I)^2 ). Je l' to sad u redu? :) Jer zato sto se uz nepoznatu X izraz nalazi sa leve strane, onda izraz koji mi je na desnoj strani jednakosti, ovo ACB-....... mnozim inverznom matricom isto sa leve strane? I jos nesto: Ovo (D-I)^2 radim kao razliku kvadrata? Izvinite sto vas gnjavim, ali uvek negde pogresim,a matrice sad radim prvi put. :(

Da, izraz koji si sada dobila je u redu.
Odgovor na naredno pitanje je takođe potvrdan.
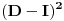
Što se tiče , treba da oduzmeš od matrice D jediničnu matricu i tako dobijenu matricu pomnožiš sa samom sobom.

E to mi je trebalo..Hvala do neba! Sad cu pokusati da zavrsim zadatak do kraja, sa datim matricama. Nadam se da cu uspeti. Hvala puno!!