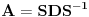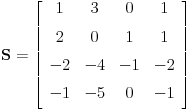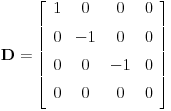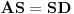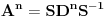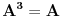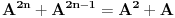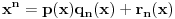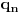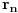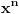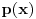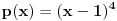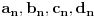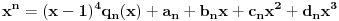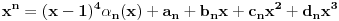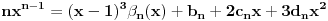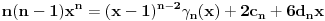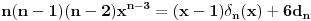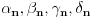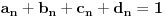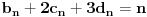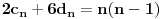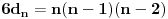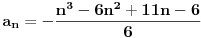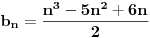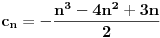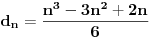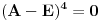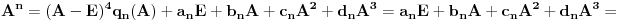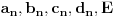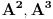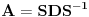
Ta formula se može koristiti samo ako svakoj sopstvenoj vrednosti odgovara onoliko linearno nezavisnoh vektora kolik je njen red. U protivnom je upotreba te formule nemoguća. Na prvu matricu se može primeniti taj postupak, tj. za

, .

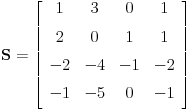
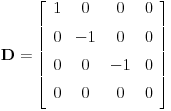
Naime, odrediš prvo sopstvene vrednosti, pa za svaku najveći broj linearno nezavisnih sopstvenih vektora, pa ih upišeš u matricu po kolonama, pa formiraš dijagonalnu matricu sa sopstvenim vrednostima po dijagonali tako da -ta vrenost na dijagonali bude sopstvena vrednost koja odgovara sopstvenom vektoru matrice koji je stavljen u -tu kolonu matrice .

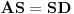
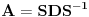
Ako si sve dobro uradio, po definiciji sopstvenih parova važi , odnosno . Na osnovu toga se indukcijom dokazuje da je .

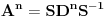
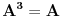
U ovom slučaju je , pa je .

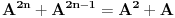
U drugom slučaju je taj postupak nemoguć jer imaš samo jednu sopstvenu vrednost i ona ima samo dva linearno nezavisna sopstvene vektora. Evo opšteg postupka:

,

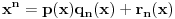
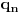
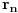
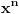
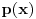
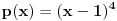
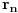
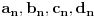
gde je količnik, a ostatak pri delenju polinoma karakterističnim polinomom (može se koristiti i minimalni). U našem slučaju je , pa pošto je nižeg stepena od , postoje konstante takve da je

.

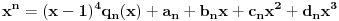
Treba ih odrediti. Diferenciranjem ove jednačine tri puta dobijamo sistem jednačina koji zajedno sa ovom glasi

,
,
,
,

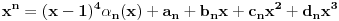
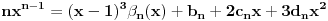
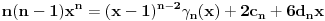
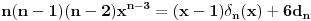
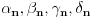
za neke polinome . Zamenom jedinicom dobijamo sistem

,
,
,
.

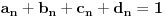
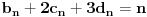
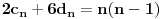
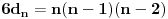
Rešavanjem ovog sistema dobijamo da je

,
,
,
.

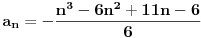
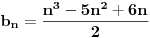
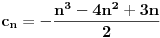
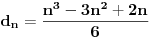
Obzirom da je

.

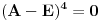
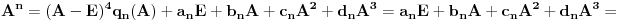
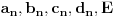
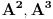
Zameni , izračunaj , sredi sve i to ti je to.