[ damir0205 @ 09.01.2013. 16:27 ] @
|
| da li mi netko moze pomoci. trebao bih funkciju y=1+a*x+b*x^2+c*x^4+d*x^6 u explicitnom obliku. Navedeni polinom predstavlja ovisnost otpora ni100 o temperaturi. Ja mjerim otpor i trebam inverznu funkciju za temp. Svaka pomoc je dobro dosla, unaprijed zahvaljujem. |
[ Nedeljko @ 09.01.2013. 19:57 ] @
Inverzna funkcija polinoma stepena većeg od jedan ne postoji jer polinom stepena većeg od jedan nije injektivan.
No, ako su ti poznati koeficijenti polinoma i zadaš neki interval na kome je on injektivan, onda se može nešto uraditi. Za polinome stepena većeg od četiri su slabe šanse da se inverz na nekom intervalu na kome je injektivan može izraziti eksplicitno, ali to obično nije ni potrebno jer postoje numeričke metode za računanje vrednosti implicitno zadane funkcije i teorema o izvodu implicitno zadane funkcije koja ti omogućava da računaš izvod. No, biće da je tebi u praksi dovoljna numerička aproksimacija inverza u vidu polinoma.
[ anonimnistefi @ 10.01.2013. 17:32 ] @
Ispravka: nijedan polinom parnog stepena nije injektivan.
S druge strane, neki polinomi neparnih stepena jesu injektivni...
[ Fitopatolog @ 10.01.2013. 20:10 ] @
Pošto je reč o temperaturnom senzoru, pretpostavljam da je u radnoj oblasti zavisnost otpora (Y) od temperature (X) jednoznačna (što bi rekao Nedeljko "injektivna") inače bi bi za dve (ili više) različite temperature senzor imao istu otpornost. Ako ovo uzmemo u obzir, do rešenja za X se lako dolazi ako znamo otpornost:
npr. neka je izmerena otpornost Y=Y1, tada se X lako može naći nekom od numeričkih metoda (npr. polovljenjem intervala).
Ne znam zašto, pade mi na pamet jedna (stara) anegdota:
Data je jedna prosečna soba kvadratne osnove. U jednom uglu se nalazi simpatična devojka. U suprotnom uglu (dijagonalno) se nalaze matematičar i inženjer njenih godina. Imaju zadatak da dođu do devojke tako što će svaki put preći polovinu rastojanja koje ih deli do nje. Matematičar odmah odustaje, znajući da će ga do devojke uvek deliti neki epsilon (preostalo rastojanje), kolikogod da je mali. Suprotno njemu, inženjer se prihvata zadatka nadajući se će epsilon posle nekog vremena moći da se zanemari...
[ Sonec @ 10.01.2013. 21:11 ] @
@Fitopatolog
Jednom sam ja pricao vrlo slican vic
http://www.elitesecurity.org/t419257-3#2934016 :)
[ Nedeljko @ 10.01.2013. 22:21 ] @
Citat:
anonimnistefi: Ispravka: nijedan polinom parnog stepena nije injektivan.
S druge strane, neki polinomi neparnih stepena jesu injektivni...
Tačno. Primer je polinom
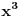
.
[ anonimnistefi @ 11.01.2013. 19:49 ] @
Citat:
Nedeljko: Tačno. Primer je polinom
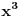
.
Exactly. :)
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.