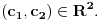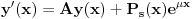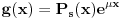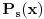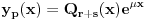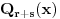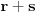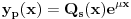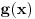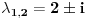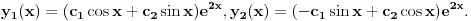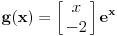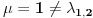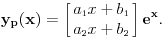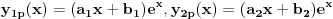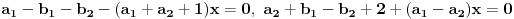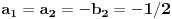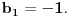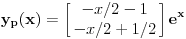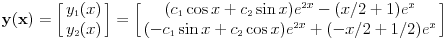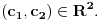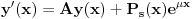
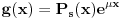
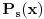
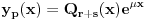
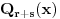
Sustina metoda je u sledecem: Neka je dat sistem of diferencijalnih jednacina u obliku . Dakle, matrica iz tvojeg zapisa je oblika , bas kako si i rekla, gde je kompleksan broj u opstem slucaju, a polinom stepena ciji su koeficijenti -dimenzionalni konstantni vektori. 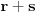Pokazuje se da ovaj sistem ima partikularno resenje u obliku , gde je red visestrukosti sopstvene vrednosti matrice , a je polinom stepena ne veceg od , sa koeficijentima koji su -dimenzionalni konstatni vektori. Ako nije sopstvena vrednost matrice , iz prethodnog sledi da je partikularno resenje oblika . 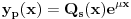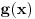Ovaj metod mozemo koristi kada slobodan clan , ima poseban naveden oblik i on nam sluzi da izbegnemo Lagranzov metod varijacije konstanti.

Evo kako konkretno koristimo ovaj metod na primeru



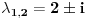
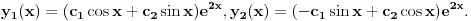
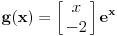
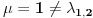
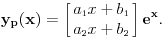
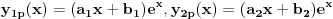
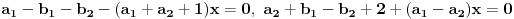
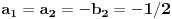
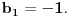
Koreni karakteristicne jednacine odgovarajuceg homogenog sistema diferencijalnih jednacina su , a opste resenje (homogenog) je dato sa Slobodan clan nehomogenog sistema je , tako da je . 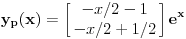Dakle, partikularno resenje negomogenog sistema diferencijalnih jednacina je oblika Zamenom () u nehomogeni sistemi DJ dolazimo do jednacina , odakle nalazimo i Prema tome, trazeno partikularno resenje je oblika , a opste resenje posmatranog sistema je dato sa ,

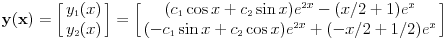
Hvala puno :)