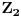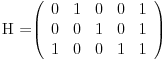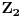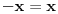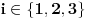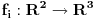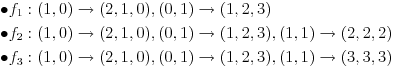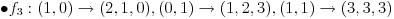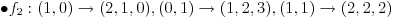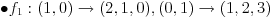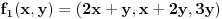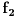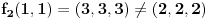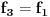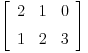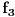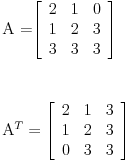[ kavens @ 22.01.2013. 14:03 ] @
|
[ kavens @ 22.01.2013. 15:58 ] @
[ Nedeljko @ 23.01.2013. 12:25 ] @
Gde si sad ventura, koji si pročitao 20-30 knjiga iz kriptografije? Neki kriptosistemi se zasnivaju na teoriji kodiranja. Ovo bi morao da znaš.
[ Nedeljko @ 24.01.2013. 08:42 ] @
Koliko vidim, tačno je
[ kavens @ 24.01.2013. 10:22 ] @
Citat: Nedeljko: Koliko vidim, tačno je Hvala puno na odgovoru. Nisam bio siguran, da li se matrica A samo obicno transportuje ili ide -A^T. [ kavens @ 24.01.2013. 15:17 ] @
[ Nedeljko @ 24.01.2013. 16:16 ] @
Pa, hajde, napiši dokle si stigao.
[ kavens @ 24.01.2013. 20:26 ] @
[ Nedeljko @ 24.01.2013. 22:15 ] @
[ kavens @ 25.01.2013. 14:29 ] @
Kako da predstavim linearno preslikavanje matricom ?
[ Nedeljko @ 25.01.2013. 15:09 ] @
[ Nedeljko @ 25.01.2013. 16:13 ] @
Ne,
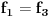 . Vektor . Vektor 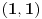 nije kanonski bazni. nije kanonski bazni.Ostatak ne mogu da uradim jer je formulacija neispravna. Citat: kavens: Za  izabrati jedno linearno preslikavanje izabrati jedno linearno preslikavanje 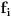 iz a. Napisati matricu A za izabrano f, trans. matricu A^T, i sve matrice B gde vazi iz a. Napisati matricu A za izabrano f, trans. matricu A^T, i sve matrice B gde vazi 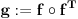 ako je ako je 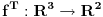 linearno preslikavanje. linearno preslikavanje.U kakvoj su vezi  i i  ? ?[ kavens @ 25.01.2013. 16:46 ] @
Citat: Nedeljko: Ne, 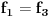 . Vektor . Vektor 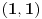 nije kanonski bazni. nije kanonski bazni.Ostatak ne mogu da uradim jer je formulacija neispravna. U kakvoj su vezi  i i  ? ?Probacu malo bolje da prevedem. b) Za  izabrati jedno linearno preslikavanje izabrati jedno linearno preslikavanje 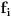 iz a. Napisati matricu A za izabrano iz a. Napisati matricu A za izabrano  , trans. matricu , trans. matricu 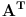 , i matricu B, koja zadovoljava , i matricu B, koja zadovoljava 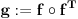 , kada je , kada je 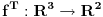 za za 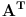 pripadajuce(odgovarajuce) linearno preslikavanje. pripadajuce(odgovarajuce) linearno preslikavanje.[Ovu poruku je menjao kavens dana 25.01.2013. u 17:58 GMT+1] [ Nedeljko @ 25.01.2013. 17:41 ] @
Bolje nemoj da prevodiš, nego prekucaj od reči do reči.
Između B i g se ne vidi ama baš nikakva veza. To je kao da si rekao "kupi takvu mačku da sutra padne kiša". [ kavens @ 25.01.2013. 17:52 ] @
 [ Nedeljko @ 25.01.2013. 19:00 ] @
E, pa onda je neka štamparska greška.
[ kavens @ 25.01.2013. 19:09 ] @
OK, hvala u svakom slucaju.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|