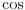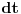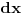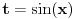|
|
[ darkjoker @ 24.01.2013. 17:41 ] @
|
| Imam zadatak,, Intg od dx/(sin^2xcos^3x) ,, i poceo sam da radim,, tj da je
tgx/2=t smena,,tj
sinx=2t/1+t^2 i
cox=1-t/1+t^2 i
dx=2/1+t^2
i zadatak mi je se previse zakomplikovao?? ima li neki puno laksi nacin,,da me usmerite??
Hvala unapred? |
[ darkjoker @ 24.01.2013. 17:42 ] @
valjda se razumije da je sin na kvadrat,,i cos na 3...da nebi bilo zabune da je 2x
[ Sonec @ 24.01.2013. 17:59 ] @
S obzirom sta Wolfram kaze, ocekivano je da se zakomplikuje. Nastavi kako si poceo.
I smena za 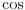 ti nije dobra, fali ti kvadrat u brojiocu. (i 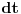 naravno kod 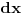 ) [ darkjoker @ 24.01.2013. 19:16 ] @
a razumijem ja ovaj princip,,dalje radeci sam dobio integral,,koji moram rjesavati integracijom racionalno,, i tako dalje,, ovaj princip mi je jasan,, samo ima previse posla,, zanima me da li postoji nesto laksi nacin,, da ovo rijesim,, ili mozda ne,, pomocu nekog trika da olaksam?? ipak hvala,, na pomoci,,znaci da sam dobro zamislio.. :D
[ Nedeljko @ 24.01.2013. 20:02 ] @
Može smenom 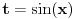 .
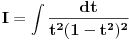 . [ different @ 25.01.2013. 10:50 ] @
a nakon ove smjene moze smjena t=1/z
[ darkjoker @ 03.02.2013. 02:00 ] @
ja sam ovaj zadatak,,pokusao rijesiti na ovaj nacin,,i puno mi je lakse,,slucajno sam se ovoga sjetio,, da ovaj integral napisemo,, ovako:
int ((cosxdx)/(sin^2xcos^4x)) =
cos^2x=1-sin^2x napisem preko formule,, i ubacim smjenu sinx=t i cosxdx=dt
i onda dobijem rjesavanje racionalne funkcije..
Ja mislim da je ovo ispravno,,da u nazivniku i brojniku dodam cosx :D ??? da li je to uredu? ako ste skontali sta sam napisao,, valjda je fino napisano??
[ darkjoker @ 03.02.2013. 13:49 ] @
Da li bi mi mogli pomoci oko jos jednog zadatka,,da ne postavljam novu temu:
imam zadtak,,koji mi je se cini laganim,medutim:
intg (sqrt(x))/(x-sqrt(x)+1)=
Ja sam prvo smjenu uveo: x=t^2 ; dx = 2tdt
i dobio:
intg (2t^2dt)/(t^2-t+1) = ????? nezz dalje :D
[ miki069 @ 05.02.2013. 12:54 ] @
U predhodnom postu si napisao da znaš integrale racionalnih funkcija.
Ovaj je 5 puta lakši od predhodnog koga kažeš da si uradio.
Prvo podeliš polinome.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|