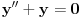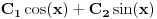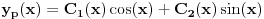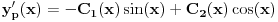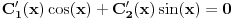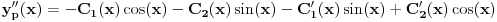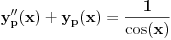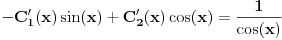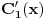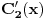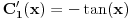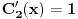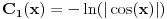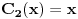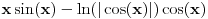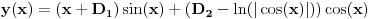[ pitagorina.teorema @ 03.02.2013. 15:10 ] @
| Imam problem sa rjesavanjem sljedeceg sistema: y'(x) = z z'(x) = -y + 1/cosx Dođem do: y''=z', sada ovo z' uvrštavam u drugu jednačinu i dobijam: y'' + y = 1/ cosx. y''+y=0 je homogena jednačina, nju znam riješiti. Međutim, nije mi jasno kako rješavam partikularni dio, tj šta radim sa ovim 1/cosx :S Takodje, zadatak tx'-x-3y = t ty' - x + y = 1 Unaprijed hvala. :) |