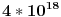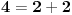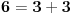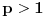Goldbahovi parovi

[ atelago @ 18.02.2013. 14:34 ] @

To niko ne zna dok ne proveri. Radi se o tome da se po hipotezi Goldbaha svaki parni
broj može napisati kao zbir dva prosta broja. Postoji jedan ili više parova prostih brojeva
koji, kad se saberu, daju zadati parni broj. Na primer, broj 10 je suma 3 + 7 i 5 + 5 ili, na
primer, broj 102 je zbir prostih brojeva: 1 i 1o1, 5 i 97, 13 i 89, 19 i 83, 23 i 79, 29 i 73,
31 i 71, 41 i 61 i 43 i 59. Ovi primeri su činjenice, ali još uvek niko nije dokazao Goldbahovu
hipotezu. Moje pitanje se odnosilo na postupak kojim se određuju svi parovi prostih brojeva
koji sabrani daju zadati parni broj kao što je pokazano za broj 102.

[ djoka_l @ 18.02.2013. 14:48 ] @

Generalno, 1 se ne smatra prostim brojem (ne znam da li neki autori ubrajaju i 1 u proste brojeve) tako da za 102 par 1,101 ne dolazi u obzir.

Drugo, do sada je Goldbahova hipoteza proverena do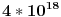

Pa ako imaš neki brz metod za nalaženje parova prostih brojeva, matematičari celog sveta će te zdušno nagraditi...

[ miki069 @ 18.02.2013. 15:58 ] @

Prost broj je prirodan broj veći od 1, deljiv samo brojem 1 i samim sobom.

Prosti brojevi su, na primer:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113,...

[ atelago @ 18.02.2013. 17:23 ] @

Dobro, dobro - sve to znamo. Pretpostavka je da su nam svi prosti brojevi u
nekom parnom broju poznati - moje pitanje se odnosi na po dva prosta broja
koji sabrani daju taj paran broj.
Ja nisam dokazao ni Goldbahovu hipotezu niti sam našao način za "generisanje"
prostih brojeva, samo sam našao zgodan način da saznam te parove, a to možda
i nije bogznašta.
Prosti brojevi i njihova svojstva su vrlo interesantna i izazovna tema pa mislim da
bilo koja novost možda može biti od značaja.
Malo mi je čudan izraz "generisanje" prostih brojeva jer oni postoje, a mi ih samo
otkrivamo. Poslednji tako otkriven broj ima preko 57 miliona cifara.

[ atelago @ 18.02.2013. 18:19 ] @

Citat:

djoka_l: Generalno, 1 se ne smatra prostim brojem (ne znam da li neki autori ubrajaju i 1 u proste brojeve) tako da za 102 par 1,101 ne dolazi u obzir.

Ako 1 nije prost broj onda Goldbahova hpoteza nije tačna jer broj 2 je paran broj
pa sledi da se ne može rastaviti na proste brojeve koji sabrani daju taj broj.

[ Sonec @ 18.02.2013. 18:31 ] @

Citat:

atelago: Ako 1 nije prost broj onda Goldbahova hpoteza nije tačna jer broj 2 je paran broj
pa sledi da se ne može rastaviti na proste brojeve koji sabrani daju taj broj.

Goldbahova hipoteza je postavljena za parne brojeve vece od dva.

[ atelago @ 18.02.2013. 19:08 ] @

U redu, čak mi se čini da sam negde naišao i na isključivanje para jednakih prostih
brojeva - problem dakle i dalje opstaje uz te korekcije.

[ Sonec @ 18.02.2013. 19:25 ] @

Lose si naisao. Takav uslov ne postoj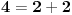i.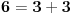

su jedina resenja za ove brojeve, drugih nema. Nego, nikako ne spominjes taj tvoj algoritam. Verovatno se plasis da ti neko ne uzme ideju, razumem.

[ igorpet @ 18.02.2013. 20:10 ] @

Ne znam da li sledeca informacija nekako pomaze, ali ako neko nije znao:

Citat:

Goldbach (Goldbah 1690-
1764) nema nikakvog značaja u matematici, izuzev što je ovaj problem poslao
Ojleru 1742. godine u pismu. On je primetio da za svaki slučaj koji je probao,
bilo koji paran broj (osim 2 koji je prost) može da se predstavi kao zbir dva
prosta broja. Na primer: 4=2+2, 6=3+3, 8=5+3, 10=5+5, 12=5+7, 14=7+7,
16=13+3, 18=11+7, 20=13+7, ....... , 48=29+19, ....... , 100=97+3, itd.
Goldbah je pitao Ojlera da li može da dokaže ovu hipotezu, ili pak da nađe
primer koji bi je opovrgao. Ojler nije uspeo da da odgovor, niti je bilo ko drugi
do danas u tome uspeo. Empirijskim proveravanjem vidimo da je ova
pretpostavka verovatno tačna. Teškoća leži u tome što su prosti brojevi
definisani preko množenja, dok se problem odnosi na sabiranje. Uopšte, teško je
utvrditi vezu između multiplikativnih i aditivnih osobina prirodnih brojeva.
Do skora, dokaz Goldbahove hipoteze izgledao je nemoguće. Danas on ne
izgleda nerešiv. Važan uspeh, veoma neočekivan i zaprepašćujući za sve
stručnjake, postigao je 1931. god. tada nepoznati, mladi ruski matematičar
Schnirelmann (Šnirerlman, 1905-1938), koji je dokazao da se svaki prirodan
broj može prikazati kao zbir ne više od 300.000 prostih brojeva. Mada ovaj
rezultat izgleda smešan u poređenju sa ciljem dokazivanja Goldbahove hipoteze,
to je ipak prvi korak u tom pravcu. Dokaz tog rastajanja za proizvoljan broj.
Nešto skorije, ruski matematičar Vinogradov, koristiće metode Hardya (Hardi)
Littlewooda (Litlvud) i njihovog velikog indijskog saradnika Ramanujana,
uspeo je da broj 300.000 smanji na 4. Ovo je mnogo bliže rešenju Goldbahovog
problema. Međutim, postoji velika razlika između Šnirerlmanovog i
Vinogradovog rezultata, veća nego što je razlika između 300.000 i 4.
Vinogradov je dokazao teoremu samo za "dovoljno velike" prirodne brojeve;
tačnije, Vinogradov je dokazao da postoji prirodan broj N takav da se svaki ceo
broj n>N može da se prikaže kao zbir od najviše 4 prosta broja. Njegov dokaz ne
omogućava da se odredi N; suprotno Šnirerlmannovom dokazu, ovaj je
indirektan i nekonstruktivan. Vinogradov je, u stvari, dokazao da pretpostavka
da beskonačno mnogo prirodnih brojeva ne mogu da se rastave na najviše 4
prosta sabirka vodi do kontradikcije. Ovde imamo dobar primer bitne razlike
između ove dve vrste dokaza, direktnog i indirektnog.
Sledeći problem, još istaknutiji od Goldbahovog, nije ni blizu rešenja.
Primećeno je da se prosti brojevi često javljaju u parovima oblika p i p+2. Takvi
su, npr., 3 i 5, 11 i 13, 29 i 31, itd. Veruje se da je tvrđenje da postoji
beskonačno mnogo takvih parova tačno, ali ni najmanji korak nije učinjen koji
bi nas probližio dokazu.

http://alas.matf.bg.ac.rs/~zlucic/view_pdf.php?id=342

[ atelago @ 18.02.2013. 20:13 ] @

3 je jedan prost broj a ne dva, odnosno par - više bih voleo da je 6 = 1 + 5,
ali da ne cepidlačimo i da ne istražujemo zašto neki ne smatraju broj 1 za prost.

Citat:

Sonec: Verovatno se plasis da ti neko ne uzme ideju, razumem.

Evo mog "algoritma" u vidu šibera. A što se tiče uzimanja ideje - valjda se i ovo
ovde smatra javnim publikovanjem koje nosi datum, a osim toga vi ste mi svedoci,
ali ne verujem da je ovo nešto naročito.

Ovo gore je slika, a za rad kliknite na donji link

[ djoka_l @ 18.02.2013. 21:03 ] @

Tvoje "rešenje" je primenljivo samo za mali opseg brojeva.

U stvari, ti si napravio mehaničku napravu koja bi se ovako prevela na kompjuterski program:

k=2*n;
for(i=3; i<=n; i+=2)
if(Prime(i) & Prime(k-i)) printf("%d+%d=%d\n", i, k-i, k);

Dakle, potrebno je da se pronađu svi prosti brojevi od 3 do n da bi se našli svi parovi prostih brojeva koji daju u zbiru 2n.

Citat:

Pretpostavka je da su nam svi prosti brojevi u nekom parnom broju poznati

Samo je ovo problem, a kao što vidiš, nije potreban nikakav mehanički šiber na kojima ćeš pisati proste brojeve, dovoljan je i kompjuter.

[ igorpet @ 18.02.2013. 21:07 ] @

Na http://members.chello.nl/k.ijntema/partitions.html imas ove parove za 10000 > n > 2.
JavaScript je u pitanju pa mozes da proucis kod ako te interesuje (http://members.chello.nl/k.ijntema/partitions.js).

A ovaj siber je varijacija ovoga:

http://en.wikipedia.org/wiki/Goldbach%27s_conjecture

_{[Ovu poruku je menjao igorpet dana 18.02.2013. u 22:23 GMT+1]}

[ atelago @ 18.02.2013. 22:06 ] @

Citat:

djoka_l: Tvoje "rešenje" je primenljivo samo za mali opseg brojeva.

Ne za mali opseg brojeva nego za malu dužinu šibera, ali ja sam rekao da je to principijelno rešenje.

Citat:

U stvari, ti si napravio mehaničku napravu koja bi se ovako prevela na kompjuterski program:

Možeš li da prepričaš šta kompjuter radi i kojim redosledom.
Na šiberu se svi parovi uparuju istovremeno bez obzira na dužinu šibera (veličinu broja)
Smatram da je ovaj princip dobijanja parova bolji od kompjuterskog jer se svi parovi
dobijaju istovremeno. Trebalo bi ga ugraditi u program ukoliko je uopšte moguće da
na ekranu kompjutera dobijemo istovremen prikaz svih parova.
Kod kompjutera postoji redosled, a ovde ga nema.
Ili ovako: Imam ogroman broj za koji mi je potreban šiber odavde do Meseca
(Što da ne? Principijelno je to dozvoljivo).
Za broj koji je za 2 manji od njega treba pomeriti jezik šibera samo za jedan podeok.
A koliko vremena bi utrošio bilo koji kompjuter da bi sračunao sve Goldbahove parove
za taj broj?
Radi se, dakle, o boljem principu.

[ zzzz @ 18.02.2013. 23:17 ] @

Ovdje bi možda bilo interesantno ubaciti takav i slične šibere.Ne zbog brzine nego zornosti.
http://www.elitesecurity.org/p193582

"@atelago:A koliko vremena bi utrošio bilo koji kompjuter da bi sračunao sve Goldbahove parove
za taj broj?
Radi se, dakle, o boljem principu."

Brže bi comp.izračunao sve te brojeve nego što bi formirao ili učitao datoteku za sliku šibera i izbacio je na ekran.
Ali ako si mislio ručno vozati neke letvice po stolu i prepisivati uočena poklapanja na komad papira,onda povlačim riječ.Tu ti priznamo da si jači.

[ atelago @ 19.02.2013. 06:51 ] @

Citat:

zzzz:
Brže bi comp.izračunao sve te brojeve nego što bi formirao ili učitao datoteku za sliku šibera i izbacio je na ekran.

U svakom slučaju kompjuter je izuzetno korisna sprava, međutim, ne treba je
toliko veličati da se ne vide prednosti nekih jednostavnih mehaničkih ostvarenja.
Parovi su na šiberu dati i ne zavise od toga da li ih čitamo i prepisujemo ili ne.
Činjenica je da ih kompjuter "računa", a šiber ne, već ih samo pokazuje.

[ atelago @ 19.02.2013. 07:32 ] @

Citat:

zzzz:
Ali ako si mislio ručno vozati neke letvice po stolu i prepisivati uočena poklapanja na komad papira,onda povlačim riječ.Tu ti priznamo da si jači.

Ne trebaju mi letvice. Nacrtao sam šiber koji radi - dakle i na kompjuteru je primenjiv
taj bolji princip s tim što za formiranje Goldahovih parova ne treba praviti nikakav program
niti "terati" kompjuter da bilo šta računa.

[ miki069 @ 19.02.2013. 07:50 ] @

Šiber se numeriše prostim brojevima.
Dakle imamo i generator prostih brojeva?
Bez generatora nema šibera odavde do meseca.

Na šiberu posle prostog broja 67 867 957 ide sledeći prost broj koji je ?? ??? ???.

[ atelago @ 19.02.2013. 08:11 ] @

@ miki069
Odgovor je dat u poruci od 18.02.2013. u 18:23

[ Nedeljko @ 19.02.2013. 09:34 ] @

Koliko ti je trebalo vremena da nacrtaš šiber za brojeve do sto i nešto? Po čemu je ovo bolji princip?

[ miki069 @ 19.02.2013. 09:59 ] @

AKo su poznati svi prosti brojevi manji od datog parnog broja, ne vidim nikakvu upotrebnu vrednost šibera.
Sve kombinacije prostih brojeva dužine 2 od 2*n elemenata koji su u zbiru jednaki 2*n, najlošiji računarski program pronalazi za 0.00001 sekundu.
Pre nego što ti šiber staviš na sto.

Dakle, bez generatora prostih brojeva, šiber i računarski program imaju upotrebnu vrednost nula.

[ Nedeljko @ 19.02.2013. 12:24 ] @

Moj laptop bez korišćenja paralelizma Eratostenovim sitom izgeneriše sve proste brojeve manje od 2³², prebroji ih i upiše na disk za minut ipo. A što se ovoga do par stotina tiče, mislim da komentar nije potreban.

[ atelago @ 19.02.2013. 14:41 ] @

Citat:

miki069
Dakle, bez generatora prostih brojeva, šiber i računarski program imaju upotrebnu vrednost nula.

To je, naravno, tačno i to niko ne osporava.

Citat:

Nedeljko: Moj laptop bez korišćenja paralelizma Eratostenovim sitom izgeneriše sve proste brojeve manje od 2³², prebroji ih i upiše na disk za minut ipo. A što se ovoga do par stotina tiče, mislim da komentar nije potreban.

Niko i ništa ne generiše proste brojeve. Ovde nije reč o otkrivanju iliti prepoznavanju
prostih brojeva (identifikovanju) već o njihovom uparivanju po Goldbahu kad su otkriveni
i nalaze se u nekom parnom broju.

[ Nedeljko @ 19.02.2013. 19:15 ] @

Hoćeš li na kraju reći za koju je namenu tvoj postupak bolji?

[ atelago @ 19.02.2013. 21:32 ] @

Ti si navodno neki programer pa napravi program!

[ pexxi92 @ 20.02.2013. 08:49 ] @

Ma vidis da Galet troluje samo ne odgovaraj mu.

[ atelago @ 20.02.2013. 09:38 ] @

Neznalice ništa ne kažu o temi ali optužuju druge da troluju.
To je ono što znaju.

[ djoka_l @ 20.02.2013. 10:42 ] @

Citat:

Ja sam našao jedan postupak koji je "istovremen" odnosno gotovo trenutan
i u principu ne zavisi od veličine zadatog parnog broja, ali da ne "trčim pred
rudu" ako je to poznata stvar.

Pokazao si nam svoj postupak koji je domišljat i koji bi mogao da pomogne u razumevanju gradiva matematike u osnovnoj ili srednjoj školi, ali ništa više od toga.
Međutim dve tvoje izjave nisu tačne:

- "u principu ne zavisi od veličine parnog broja", zavisi i to mnogo, postupak važi samo za parne brojeve koje su u opsegu šibera i za bilo koji proizvoljno veliki šiber, prvi veći parni broj ne može da se razloži na dva prosta sabirka.
- "gotovo trenutan" je pogrešno, šiber je brz za male parne brojeve, ali svaki računar sa čak loše napisanim programom, to radi mnogo brže. Za opseg brojeva koji je problem da se uradi na računaru, šiber uopšte ne radi.

Evo, ja ti odajem javno priznanje na tvom izumu, uz napomenu da je to ipak samo igračka koja demonstrira na lep način jedan matematički problem i metod za njegovo rešavanje na malom opsegu.

EDIT: A, da - tvoj šiber ima bag, ne treba da bude broj 1 na šiberu, a broj 2 fali. Zato šiber pronalazi rešenje 4=1+3, koje nije dobro, ali ne pronalazi 4=2+2 koje je ispravno...

[ Nedeljko @ 20.02.2013. 10:58 ] @

Citat:

atelago: Neznalice ništa ne kažu o temi ali optužuju druge da troluju. To je ono što znaju.

Pa, u pravu je. Na pitanje za koju je namenu tvoj postupak bolji odgovaraš sa zahtevom da napišem neki program. Koji program? Za šta? Kakve veze ima pisanje programa sa prednostima tvog šibera?

Citat:

djoka_l: Pokazao si nam svoj postupak koji je domišljat i koji bi mogao da pomogne u razumevanju gradiva matematike u osnovnoj ili srednjoj školi, ali ništa više od toga.

Šta je tu domišljato? Šiber postoji odavno. Njime se i sabira i oduzima i množi i deli i računaju eksponenti i logaritmi. On je uzeo poznato sabiranje/oduzimanje na šiberu i sav izum je u tome da je označio proste brojeve na skalama šibera.

[ atelago @ 20.02.2013. 14:24 ] @

Citat:

Nedeljko:
Pa, u pravu je. Na pitanje za koju je namenu tvoj postupak bolji odgovaraš sa zahtevom da napišem neki program. Koji program? Za šta? Kakve veze ima pisanje programa sa prednostima tvog šibera?

Odlutao si! Kako "Koji program"? Pa program za iznalaženje parova prostih brojeva
koji sabrani daju zadati paran broj. Napravi program pa ćeš da vidiš kakve veze ima
sa šiberom.
Ti kao i pexxi92 pričaš oko teme a ne o temi, a da napraviš program verovatno
ne umeš pa se vadiš pitanjem "Kakav program?".

Citat:

djoka_l:- "u principu ne zavisi od veličine parnog broja", zavisi i to mnogo, postupak važi samo za parne brojeve koje su u opsegu šibera i za bilo koji proizvoljno veliki šiber, prvi veći parni broj ne može da se razloži na dva prosta sabirka.

Ipak treba da razmisliš šta znače reči "u principu" u odnosu na tvoju konkretizaciju.
Konkretan šiber nije bogznašta, ali je princip povoljniji od od izračunavanja nekim
redosledom što je princip kod kompjuterskog računanja, a po ovom principu (koga ja
nisam izmislio) dobijaju se svi parovi istovremeno.

Citat:

EDIT: A, da - tvoj šiber ima bag, ne treba da bude broj 1 na šiberu, a broj 2 fali. Zato šiber pronalazi rešenje 4=1+3, koje nije dobro, ali ne pronalazi 4=2+2 koje je ispravno...

Dobro, ali to nije neka važna primedba niti zamerka principu, iako se nisi potrudio
da pokažeš zašto 1 nije prost broj.

[ djoka_l @ 20.02.2013. 14:39 ] @

http://en.wikipedia.org/wiki/Prime_number

Citat:

A prime number (or a prime) is a natural number greater than 1

http://mathworld.wolfram.com/PrimeNumber.html

Citat:

A prime number (or prime integer, often simply called a "prime" for short) is a positive integer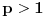

Citat:

The number 1 is a special case which is considered neither prime nor composite (Wells 1986, p. 31). Although the number 1 used to be considered a prime (Goldbach 1742; Lehmer 1909, 1914; Hardy and Wright 1979, p. 11; Gardner 1984, pp. 86-87; Sloane and Plouffe 1995, p. 33; Hardy 1999, p. 46), it requires special treatment in so many definitions and applications involving primes greater than or equal to 2 that it is usually placed into a class of its own.

Da li imaš link na neki izvor koji ubraja 1 u proste brojeve? Jednostavno, to je konvencije da je najmanji prost broj 2.

Citat:

Dobro, ali to nije neka važna primedba niti zamerka principu, iako se nisi potrudio
da pokažeš zašto 1 nije prost broj.

Ne ynam da li je principijelna zamerka, ali je činjenica da je broj 2 prost, a ne nalazi se na tvom šiberu, te tako šiber ne pronalazi sve kombinacije prostih sabiraka. Da bi se 2 dodao, verovatno bi morali da se dodaju i svi ostali parni brojevi.

Znaš, kada pravim program, pa moj program radi za sve zahtevane brojeve u opsegu prihvatljivih brojeva, a ne radi za jedan broj, onda se kaže da program ne radi dobro, bez obzira što on "principijelno" radi dobro.

[ Nedeljko @ 20.02.2013. 15:05 ] @

Program je banalan. Evo ga:

Code (cpp):

#include <cstdlib>

#include <iostream>

using namespace std;

bool prime(int p)

{

     for (int i = 2; i < p; ++i) {

          if (p%i == 0) {

               return false;

          }

     }

     return true;

}

int main()

{

     int n;

     do {

          cout << "Enter the even integer greater than 2: " << flush;

          cin >> n;

     } while (n <= 2 || n%2 == 1);

     for (int p = 2; p < n - 1; ++p) {

          if (prime(p) && prime(n - p)) {

               cout << n << " = " << p << " + " << n - p << "." << endl;

          }

     }

     return EXIT_SUCCESS;

}

No, i dalje ne vidim nikakvu prednost tvog šibera.

Ako neko može da bira između ovog programa i tvog šibera, zašto bi se opredelio za šiber?

_{[Ovu poruku je menjao Nedeljko dana 21.02.2013. u 08:59 GMT+1]}

[ Nedeljko @ 20.02.2013. 15:07 ] @

atelago,

Da broj 1 nije prost se ne pokazuje, već je to konvencija.

[ djoka_l @ 20.02.2013. 15:10 ] @

Citat:

Principijelno, jednostavnije je meriti rastojanje Zemlja - Mesec ovim:

[ Nedeljko @ 20.02.2013. 15:32 ] @

Jedina prednost ovog šibera je što je lakše proizvesti njega nego kompjuter.

[ igorpet @ 20.02.2013. 16:26 ] @

Pa sad, ako cemo o prednostima ... lakse je imati papir (veci ili manji), par lenjira (u skladu sa velicinom papira) i olovku i nacrtati ovo:

Ovde nema pokretnih delova a odmah se vidi i rezultat i to za svaki paran broj.
Mislim da je bolje od sibera po funkcionalnosti, mada nisam ovo ja izmislio ...

[ atelago @ 20.02.2013. 18:14 ] @

@djoka_l
Ukoliko je to konvencija za broj 1 to je onda nešto drugo, ali po prirodi prostih
brojeva taj broj treba da se smatra prostim jer on sabran sa bilo kojim drugim
prostim brojem daje paran broj kao što je to slučaj i sa svim ostalim prostim
brojevima. Broj 2 jeste prost broj po nekim svojstvima, a po nekim nije.
Deljiv je sa jedan i sa samim sobom, ali je jedini paran broj među prostim
brojevima, a osim toga sabran sa bilo kojim prostim brojem ne daje paran
broj. U tretiranju prostih brojeva, po mom mišljenju, trebalo bi isključiti
broj 2 jer ako gledamo niz prostih brojeva očigledno je da se tu ne uklapaju
ni 2 ni 0. Ali to je druga tema i druga dilema.
@Nedeljko
Ja sam tek nešto malo načuo o programiranju pa se izvinjavam ako grešim.
U programu imaš neku petlju jer stoji reč "for..." pa pretpostavljam da se
time tretiraju neki brojevi po nekom redosledu, a i vremenski termin "while"
što upućuje na to da se neki brojevi tretiraju pre drugih, a samim tim i
rezultati se dobijaju u različita vremena, odnosno, neki parovi treba da
sačekaju dok na njih dođe red.
Kod šibera nije tako - svi parovi se "tretraju" istovremeno - ni jedan par
se ne iskazuje pre bilo kog drugog ni posle bilo kog drugog.
Brzina rada kompjutera jeste impozantna, ali ma kolika bila ta brzina ona
zahteva vreme između određivanja dva uzastopna para prostih brojeva.
U tome je bitna principijelna razlika, jer ako bismo taj princip istovremenosti
upotrebili kod kompjutera on bi višestruko brže davao tražene podatke.
U sledećoj pruci pokušaću to i da pokažem slikom.
@igorpet
Nije ni bolje ni preglednije jer tu su dati parovi za neki niz parnih brojeva
zajedno iliti tu su već izračunati i napisani rezultati za sve parne brojeve
nekog niza t. j. tu možeš da nađeš nešto što je neko već izračunao
odnosno prikazao.
Kod programa ili kompjutera sračunavaju se i prikazuju rezultati za neki
zadati parni broj.

[ pexxi92 @ 20.02.2013. 18:21 ] @

Ok, prozivas ljude neznalicama a pokazujes elementarno nepoznavanje i samog problema a kamoli resenje. Prvo bunis se oko toga dal je 1 prost broj (LOL), neznas tacnu formulaciju Goldbahove hipoteze a posebno pojma nemas o slozenosti izracunavanja itd. Dakle uz eratostenovo sito ili bilo koju funkciju koja proverava da li zadatai broj prost implementacija je trivijalna. Ti si decko neko ko je stao na osnovnom ili nekom ranom srednjem obrazovanju i smatras da ti je to dovoljno da resavas kompleksne probleme sto se videlo i na mnogim ranijim temama gde si pokazao elementarno nepoznavanje nekih osnovnih principa iz raznih oblasti/nauka. Ako stvarno zelis nesto da postignes prvo prouci ono sto su do sada ljudi radili i rezultate koje su dobijali a onda predlazi svoja briljijantna resenja.
Tolko od mene...

[ igorpet @ 20.02.2013. 18:36 ] @

Citat:

atelago:
...
@igorpet
Nije ni bolje ni preglednije jer tu su dati parovi za neki niz parnih brojeva
zajedno iliti tu su već izračunati i napisani rezultati za sve parne brojeve
nekog niza t. j. tu možeš da nađeš nešto što je neko već izračunao
odnosno prikazao.
Kod programa ili kompjutera sračunavaju se i prikazuju rezultati za neki
zadati parni broj.

Nisu napisani i izracunati nego su geometrijski dobijeni (u preseku plave, crvene i sive linije) i ovim postupkom mozes da nadjes rezultate za onoliko parnih brojeva za koliko smo ucrtali.
Metod je jednostavniji za rad jer kad jednom shvatimo princip mozemo ga uvek ponoviti (nacrtati) a siber nije lako napraviti i jos je nejasno kako odredjujemo "praznine" i kada pocinje javljanje dupliranih rezultata. Ovde tih pitanja nema jer se sve vidi jednim pogledom.
Ali teze je objasniti recima, nego pogledati sliku jer se princip lako uocava.

Nacrtamo linije pod nekim uglom, obelezimo ih neparnim brojevima redom a zatim izbacimo linije tj. brojeve koji nisu prosti
ili za bojeve koji nisu prosti ne vucem liniju ali im predvidimo mesto.
Isto to uradimo sa linijama koje su sa druge strane pod suprotnim uglom.
Povucemo horizontalne linije (ali samo od sredine ili levo ili desno), obelezimo parne brojeve i u preseku su rezultati.
Ne moramo uvek da krecemo sa crtanjem od pocetka, mozemo krenuti od nekog proizvoljnog dela ali moramo znati gde je pocetak.

Geometrijske metode su uslovljene prostorom za crtanje, ali ni sa siberom nije mnogo drugacije.
Objasni sada ti postupak obelezavanja sibera, pa ce se videti sta je jednostavnije.

[ Nedeljko @ 20.02.2013. 18:57 ] @

atelago

Ima još bolji metod od tvog šibera - uzmeš svesku i za svaki paran broj do nekog napišeš sva njegova rastavljanja. Posle tu svesku koristiš koliko puta hoćeš.

[ atelago @ 20.02.2013. 20:16 ] @

Pa valjda i sam vidiš da to nije bolji metod.

[ atelago @ 20.02.2013. 20:27 ] @

Evo još malo prikazivanja i poređenja različitih principa

[ Nedeljko @ 20.02.2013. 22:42 ] @

Citat:

atelago: Pa valjda i sam vidiš da to nije bolji metod.

A zašto nije? Kao što moraš da praviš šiber, moraš i da ispišeš svesku. Isto tako, sva rastavljanja su istovremeno prikazana i to za sve parne brojeve čija su rastavljanja uneta u svesku.

[ atelago @ 21.02.2013. 06:19 ] @

Citat:

Nedeljko: A zašto nije? Kao što moraš da praviš šiber, moraš i da ispišeš svesku. Isto tako, sva rastavljanja su istovremeno prikazana i to za sve parne brojeve čija su rastavljanja uneta u svesku.

Pa moraš da napraviš i kompjuter a to je daleko teži posao od pravljenja šibera.
Upoređivanje sveske sa šiberom ili kompjuterom je još gore nego sabiranje baba i žaba.
Kompjuter sračunava i uparuje proste brojeve a šiber samo uparuje.
Sveska ne radi ništa od toga. Odakle potiču ti podaci ispisani u svesci? Prepisani
su rezultati koje je dao kompjuter ili šiber ili neko drugi.
Sveska nije uređaj pomoću koga otkrivamo Goldbahove parove prostih brojeva.
Besmisao tvog upoređivanja možeš da vidiš i po ovome: zašto da računamo proizvode
prirodnih brojeva kad možemo lepo da sve rezultate upišemo u svesku i ne treba nam
više ni kompjuter ni šiber ni računaljka sa kuglicama.
U tvom nastojanju da po svaku cenu bagatelišeš moje poređenje dvaju različitih principa
konstruišeš besmislene izjave i tvrdnje napuštajući u potpunosti principijelan pristup
problemu.

[ Nedeljko @ 21.02.2013. 09:29 ] @

Citat:

atelago: zašto da računamo proizvode
prirodnih brojeva kad možemo lepo da sve rezultate upišemo u svesku i ne treba nam
više ni kompjuter ni šiber ni računaljka sa kuglicama.

Zato što za opseg brojeva koje računar može da množi za manje od jedne sekunde ne bi bila dovoljna ni sveska veličine svemira.

Poenta sa sveskom je da u nju staju tablice za mali opseg vrednosti ili za mali broj vrednosti. Nekada su se takve sveske koristile i zvale su se logaritamske tablice. Naravno, sa pojavom kalkulatora su izgubile smisao.

[ igorpet @ 21.02.2013. 09:56 ] @

Imamo zadatak ko neko treba da resi (na casu, takmicenju, ispitu, ...):
- Naci sve Goldbahove parove za brojeve od 41 do 49. Koliko ima takvih parova?

Kako ce to neko na najbolji nacin resiti ako na raspolaganju ima papir, olovku, hemijsku, dva lenjira i sestar (ono sto je inace dozvoljen pribor)?
Podrazumeva se da racunar nije dozvoljen (ali moze da ga napravi od raspolozivog materijala), ostala pomocna sredstva takodje (ako moze da ih napravi od raspolozivog materijala).
Ja sam izlozio moj pristup (koga nisam ja osmislio) kako bi mogli ovo da resimo (relativno jednostavno za nekih max 20 min)
- Erastotenovim sitom odredimo sve proste brojeve do 49 (mada realno moze i do 43 jer je 48=43+5 ali da ne bi gubili vreme oko razmatranja uzmemo veci broj odmah)
- geometrijskim izlozenim postupkom nadjemo resenja (da se ovo nacrta ne treba vise od 15-ak minuta).

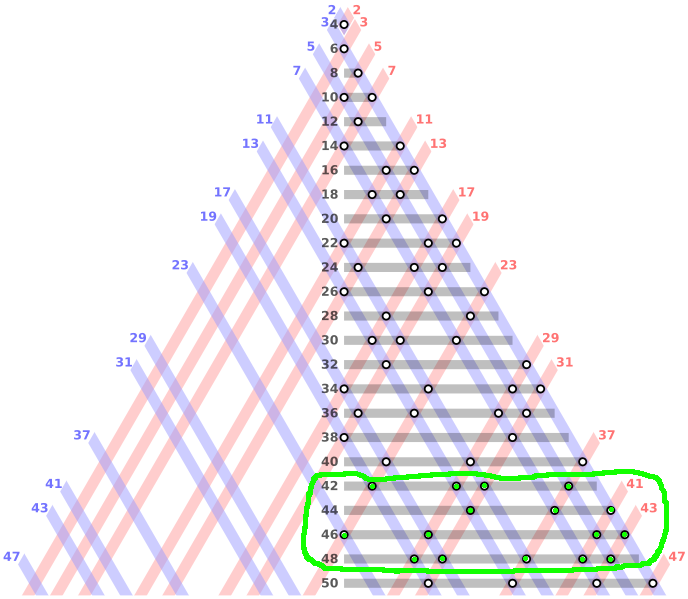
Postupak je univerzalan i za vece brojeve ali se potrebno vreme i prostor za crtanje geometrijski uvecavaju.

Ako moze siber da se nacrta i improvizuje za manje vreme onda ce to biti bolje resenje.
Pitanje je kako mozemo siber da nacrtamo (improvizujemo)?
Ja nisam uspeo da uocim princip (mada se detaljno nisam ni bavio time) ali nije uocljiv na prvi pogled kao ovo geometrijsko resenje.

Za neke inzenjerske potrebe siber ce biti upotrebljiv koliko i tablice, a racunar daleko delotvorniji.

A diskusija bi mogla da bude ipak malo konstruktivnija nego sto jeste.

[ atelago @ 22.02.2013. 14:09 ] @

@igorpet

Ima li jednostavnije od ovoga - ispišeš niz neparnih brojeva u jednom smeru
na jednom papiru pa onda ispišeš taj isti niz u suprotnom smeru na drugom
papiru - proste brojeve u oba niza nekako istakneš (ili nekom bojom ili boldovanjem)

Sad papire postaviš jedan pored drugog i vozaš po volji. Uvek ti se po vertikali neki
prosti brojevi podudaraju i daju parni zbir koji želiš i koji je jednak zbiru zelene jedinice
sa brojem iznad nje. Na slici je prikazan položaj nizova za određivanje parova broja 72

Ovo nije baš pregledno zato pogledaj ovaj prilog:

[ atelago @ 22.02.2013. 14:26 ] @

Citat:

Nedeljko: Zato što za opseg brojeva koje računar može da množi za manje od jedne sekunde ne bi bila dovoljna ni sveska veličine svemira.

Pretera li ga pretera! I ko te pita za množenje? Ovde poredimo dva principa - pa računar
koji radi na principu redosleda je daleko sporiji od računara koji bi radio po takvom principu
kakav je kod šibera.

[ Nedeljko @ 22.02.2013. 14:59 ] @

Kako ko pita za množenje? Pročitaj citat na koji je to bio odgovor.

Baš me zanima kako bi izgledao računar koji radi na principu šibera. Što li ljudi ne množe i dan danas na šiberu?

[ igorpet @ 22.02.2013. 16:24 ] @

Citat:

atelago:
...
Ima li jednostavnije od ovoga - ispišeš niz neparnih brojeva u jednom smeru
na jednom papiru pa onda ispišeš taj isti niz u suprotnom smeru na drugom
papiru - proste brojeve u oba niza nekako istakneš (ili nekom bojom ili boldovanjem)

Sad papire postaviš jedan pored drugog i vozaš po volji. Uvek ti se po vertikali neki
prosti brojevi podudaraju i daju parni zbir koji želiš i koji je jednak zbiru zelene jedinice
sa brojem iznad nje.

Slazem se, ovo je jednostavniji princip za pronalazenje Goldbahovih parova.
Dovoljan je samo papir i olovka u dve boje (ili hemijska i olovka), lako se improvizuje, trazi manje prostora na papiru od geometrijskog i brze mozemo odraditi.
Nadam se da ce princip posluziti nekome.
Resenje gornjeg problema ovom metodom:

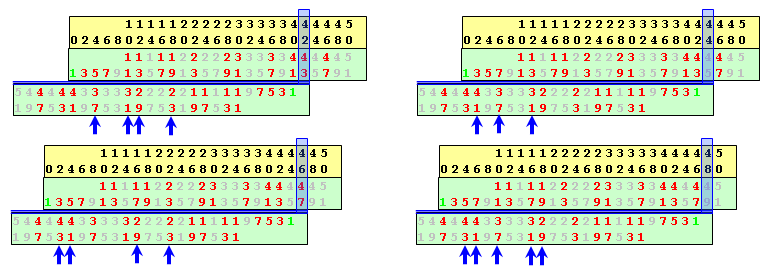
[ Nedeljko @ 22.02.2013. 17:39 ] @

Ja mislim da je poenta ovog izuma što ga je Dane smislio.

Bravo Dane, majstore! Kako si ti pametan.

[ atelago @ 23.02.2013. 07:05 ] @

Citat:

Nedeljko:
Baš me zanima kako bi izgledao računar koji radi na principu šibera.

Pa pokazao sam ti nešto u tom smislu u poruci od 20. 2. u 21:27, ali nisam
baš sve - ostavio sam i tebi da nešto smisliš!

Citat:

Što li ljudi ne množe i dan danas na šiberu?

Šiber je približna računica za računske operacije koje se na njemu rade,
ali moj predlog za prikaz Goldbahovih parova je 100% tačan.

[ igorpet @ 23.02.2013. 11:49 ] @

Pored tvrđenja da:
-Svaki paran broj veći od 2 može da se napiše kao zbir dva prosta broja

Postoje još neka tvrđenja:
-Svaki ceo broj veći od 5 može da se napiše kao zbir tri prosta broja

tj. ovo tvrđenje se može razbiti na:
- Svaki paran broj veći od 4 može da se napiše kao zbir tri prosta broja
- Svaki neparan broj veći od 5 može da se napiše kao zbir tri prosta broja

Postoji i, na prvi pogled, sličan problem koji se suštinski razlikuje:
-Svaki paran broj može da se napiše kao razlika dva prosta broja (Minus-Goldbach pairs www.pantonov.com/thoughts/goldbach-minus.php)

@atelago da li si se bavio i ovim problemima?