[ nikolinv @ 28.02.2013. 20:37 ] @
| Neka je A'B'C' trougao, dobijen rotacijom trougla ABC oko tačke O (centra opisane kružnice). Suprotne tačke preseka stranica ova dva trougla su konkurentne. Zašto? 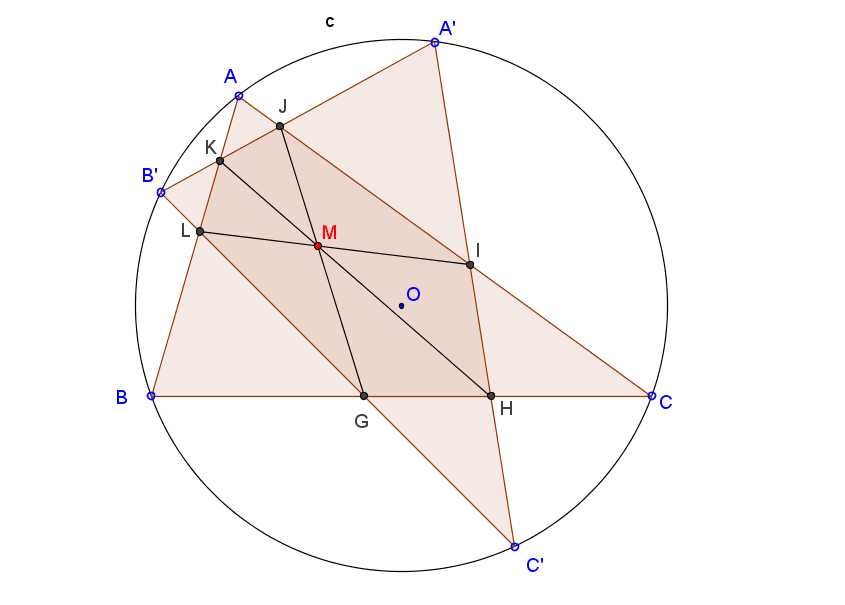 |
|
[ nikolinv @ 28.02.2013. 20:37 ] @
[ Nedeljko @ 02.03.2013. 14:11 ] @
Zato što se temena oba trougla nalaze na istom konusnom preseku. To je jedino što je bitno. Ovo je stav nalik na Brianšonovu teoremu i može se na sličan način dokazati.
Dakle, ako tačke A i B u ravni imaju homogene koordinate 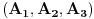 i i 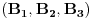 , onda prava kroz njih ima homogene koordinate , onda prava kroz njih ima homogene koordinate 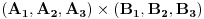 , gde je , gde je 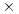 operacija vektorskog proizvoda na operacija vektorskog proizvoda na 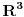 . Isto važi i za homogene koordinate presečne tačke dveju pravih kojima su date homogene koordinate. . Isto važi i za homogene koordinate presečne tačke dveju pravih kojima su date homogene koordinate. Uslov da tačke čije su homogene koordinate  (svako (svako 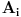 je jedna trojka realnih brojeva) pripadaju istom konusnom preseku je je jedna trojka realnih brojeva) pripadaju istom konusnom preseku je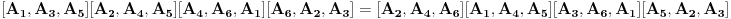 a uslov da je trojka pravih konkurentna je da je mešoviti proizvod njihovih homogenih koordinata jednak nuli. [ Nedeljko @ 03.03.2013. 01:55 ] @
Pozivaću se na stavove iz ovog članka:
http://www.ias.ac.in/mathsci/vol120/nov2010/pm-10-00024.PDF Prema Brianšonovoj teoremi, dovoljno je dokazati da prave na kojima leže strane trouglova pripadaju istoj krivoj druge klase, odnosno da su tangente na isti konusni presek. Numerišimo ih na sledeći način: 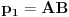 , , 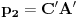 , , 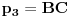 , , 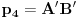 , , 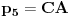 , , 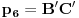 , ,Dakle, treba dokazati da je 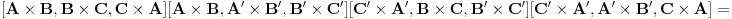 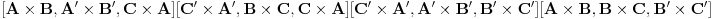 . .Obzirom da je 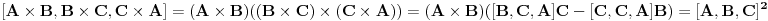 , ,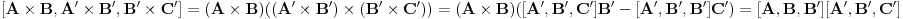 , ,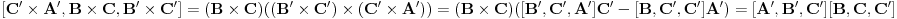 , ,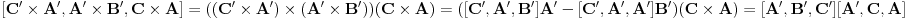 , ,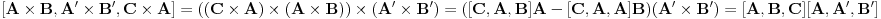 , ,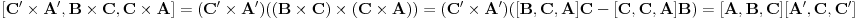 , ,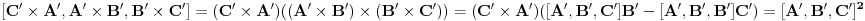 , ,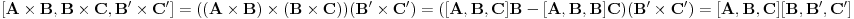 , ,jednakost koju treba dokazati glasi 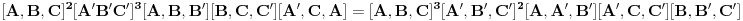 . .Ona je posledica jednakosti 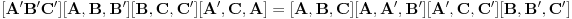 . .pa je dovoljno nju dokazati. Numerišući temena dvaju trouglova na sledeći način: 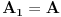 , , 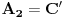 , , 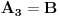 , , 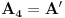 , , 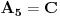 , , 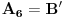 , ,dobijamo da uslov pripadanja ovih tačaka jednom konusnom preseku glasi 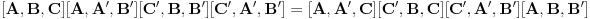 . .Ovaj uslov je ispunjen jer po pretpostavci temena trouglova pripadaju istom konusnom preseku, a taj uslov je ekvivalentan onome koji je potrebno dokazati. [ Nedeljko @ 04.03.2013. 03:17 ] @
Smem li da znam odakle ovaj zadatak?
[ nikolinv @ 04.03.2013. 20:31 ] @
Pre svega, hvala na trudu, Nedeljko. Problem je originalno iz geometrije konika, a ja sam pokušao da ga prevedem u euklidsku geometriju, pa da ga tako rešim, što mi, nažalost, nije uspelo. Ne baratam analitičkim alatkama, koje ti koristiš, već me zanima sintetički pristup. Evo originala, pa ako ti možeš da pomogneš, hvala ti:
My original problem was: Let c is a conic, ABCDEF is a Pascal hexagon(6 points on the conic c), sides of triangles ABC and DEF intersect pairwise in points IJKLMN. I found using GeoGebra, that lines IJ, KL and MN are concurrent in point S (inside a conic). Is it Steiner point? I found (6*5*4)/(3*2*1)=20 points, choosing pairs of triangles among 6 points. Number of Steiner points is also 20, but ABCDEF, ACDFEB, ACBEDF is not a configuration in article about Steiner points, so i cant prove this beautiful... Theorem:Let ABC and DEF be two triangles lie on a conic and points IJKLMN are pairwise intersections of it's sides. Then opposite vertices of this hexagon are concurrent. Vice cersa is also true. Do you know something about that? 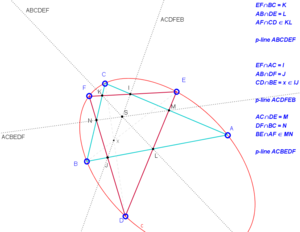 [ Nedeljko @ 04.03.2013. 20:47 ] @
Korišćene analitičke alatke su izložene u navedenom članku, naravno ako engleski nije problem.
Citat: nikolinv: Theorem:Let ABC and DEF be two triangles lie on a conic and points IJKLMN are pairwise intersections of it's sides. Then opposite vertices of this hexagon are concurrent. Upravo sam ovu formulaciju dokazao. E, sad, ima li ta teorema neko ime, pa da je nađemo? [ nikolinv @ 04.03.2013. 21:36 ] @
Ne znam ime ali ima ekvivalencija: "It is known that if the vertices of two triangles are on the same conic then the sides of these triangles are the tangents of another conic." Posle samo Brianšon.
Evo jednog dokaza: We use Steiner's famous theorem, which states - together with its converse - that the points A, B, C, D, E, F are on a conic if and only if the cross ratios of the lines 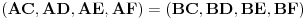 . The dual of this theorem gives that the lines a, b, c, d, e, f are tangents of a conic if and only if the cross ratios of the points . The dual of this theorem gives that the lines a, b, c, d, e, f are tangents of a conic if and only if the cross ratios of the points 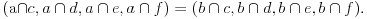 So, using the notations of your figure, (BA,BC,BA',BC')=(B'A,B'C,B'A',B'C'). Intersecting the first four lines by A'C' and the second four lines by AC we get that 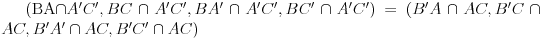 . .Here 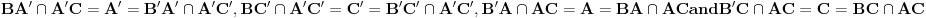 , so this means that , so this means that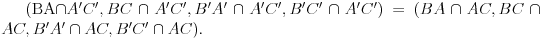 Thus by the above mentioned theorem there is a conic whose tangents are A'C', AC, BA, BC, B'A' and B'C'. [ nikolinv @ 04.03.2013. 22:01 ] @
Citat: Nedeljko: Korišćene analitičke alatke su izložene u navedenom članku, naravno ako engleski nije problem. Engleski je ovde najmanji problem Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|