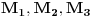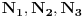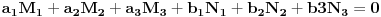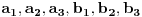[ dukowski @ 21.03.2013. 19:40 ] @
| [img=http://s24.postimg.org/ez01wxmch/Zadatak.jpg] Da li su dva zadata prostora zapravo dva trodimenzionalna prostora čije tri matrice predstavljaju tri ravni u svakom od njih koje i čine te 3D prostore (svaka matrica sa svoje dvije jednačine pravih koje se mogu formirati od koeficijenata kolona predstavlja ravan koju određuju te dvije prave), pa traženi presjek i zbir potprostora čine takođe trodimenzionalni prostori? Da li se onda tražene baze presjeka i zbira dobijaju tako da: 1. da se dobije presjek dva prostora S i T, elementi jednog i drugog prostora se izjednače, pa se od tako dobijenih jednačina dobijaju kolone baza presjeka, npr. 2*x + 0*y = -7*x + 1*y -> 9*x - 1*y=0 1*x + 3*y = 2*x - 6*y -> -1*x + 9*y=0 Pa je matrica prvog od tri elementa baze presjeka: 9 -1 -1 9 2. da se dobije zbir dva prostora S i T elementi jednog i drugog prostora se saberu, pa se od tako dobijenih jednačina dobijaju kolone baza zbira, npr 2*x + 0*y + ( -7*x + 1*y ) = 0 -> -5*x + 1*y=0 1*x + 3*y + 2*x - 6*y = 0 -> 3 3*x - 3*y=0 Pa je matrica prvog od tri elementa baze zbira: -5 1 3 -3 itd za ostale elementa baze presjeka i baze zbira. [Ovu poruku je menjao dukowski dana 21.03.2013. u 20:51 GMT+1] |