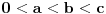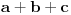[ Janinka @ 26.03.2013. 19:43 ] @
Ovako, imam jedan zadatak da rešim, a ja ne znam ni odakle da počnem. Dobro bi mi došla bilo kakva pomoć, a može i preko PP.

U jednoj grupi glasača za gradonačalnika, na broju žele glasati za kandidata A, za kandidata B i za kandidata C, i još . U predizbornom muku nije dozvoljeno skupljanje u grupama koje broje više od dvojice glasača koji bi diskutovali oko kandidata. Uvek kad dođe do susreta između bilo kojih dvojice glasača iz različitih tabora, posle diskusije i datih obrazloženja dvojica menjaju svoje ubeđenje i glasali bi za trećeg kandidata. Tako, ako se susretnu dvoje koji bi pre susreta glasali za kandidate A i B, posle razgovora obojica odluče da glasaju za kandidata C. Ako potom neki od njih susretne drugog glasača koji bi glasao za kandidata A, posle razgovora oboje bi glasali za kandidata B.
Pitanje je dali se može desiti da se svih glasača ubede da glasaju za istog kandidata?
[ zzzz @ 27.03.2013. 14:05 ] @
Citat:
Janinka: 
Pitanje je dali se može desiti da se svih glasača ubede da glasaju za istog kandidata?


Da,ali ne za sve kombinacije brojeva.Naprimjer za 1,2,5 sretnu se a i c pa imamo 0,4,4,a zatim b i c naprave 8,0,0.
Za 1,2,3 ne ide.Dakle ima skupova 0<a<b<c za koje to ne ide.Koji su to skupovi?
[ nikolinv @ 28.03.2013. 12:33 ] @
- Kada A i B povećaju C, on se poveća za dva, oni se smanje za jedan. Razlika između A i B ostaje ista, ali razlika između A i C (B i C) se promeni za tri.

- Pošto u konačnoj konfiguraciji tražimo da npr. A=B=0, nju ćemo dobiti (ako i) samo ako je bar jedna od međusobnih razlika deljiva sa tri.

- Zato 1,2,3 ne radi , a 1,2,5 (5-2=3) radi.
[ Picsel @ 28.03.2013. 13:30 ] @
Citat:
nikolinv:
- Pošto u konačnoj konfiguraciji tražimo da npr. A=B=0, nju ćemo dobiti (ako i) samo ako je bar jedna od međusobnih razlika deljiva sa tri.


A sta sa A = 1, B = 2, C = 8?
[ nikolinv @ 28.03.2013. 14:21 ] @
(1,2,8)->(3,1,7)->(2,3,6)->(4,2,5)->(3,4,4). Dalje za domaći.

Ako analiziramo prikazani postupak, dolazimo do sledećeg zaključka:

Teorema: Svaka "neispravna" konfiguacija se može svesti na oblik: (a,a+1,a+2).

Sledi da neispravne konfiguracije imaju zbir deljiv sa 3. Očigledno ne važi i obrnuto.
[ Janinka @ 29.03.2013. 12:17 ] @
Hvala svima!!!! Pozdrav!!!!