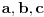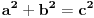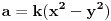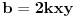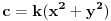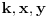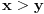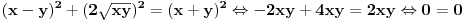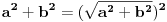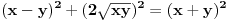|
|
[ number42 @ 01.04.2013. 01:37 ] @
|
| pozdrav.
hteo sam da pitam da li postoji nesto kao opsta formula za pitagorinu teoremu, jer nisam cuo za nju. matematika me zanima ono cisto kao hobi, i sa srednjoskolskim znanjem otprilike.
dok sam zvrljao onako bezveze, dobio sam neku formulu al ne znam da li vec postoji tako nesto. trazio sam po netu ali nisam nasao.
bila bi u obliku ovako nekako:
(x-y)^2+(2sqrt(xy))^2=(x+y)^2
dakle sa dve promenljive.
iz toga se lagano izvlaci i opsta formula za stranice bilo kog nepravouglog trougla, takodje sa dve promenljive:
a=x
b=x+y
c=sqrt(y^2+(2sqrt(xy))^2)
znaci, da li vec postoji ovako nesto, i ima li ovo uopste nekog znacaja, tj da li se moze primeniti?
hvala. |
[ number42 @ 01.04.2013. 06:33 ] @
ehmm... drugi deo nije tacan. valjda sam u brzini pogresio ovo za stranice trougla.
ali prvi deo, opsta formula, je tacna, jer dokaz je jako prost. u klasicnoj formuli za pitagorinu teoremu a^2 +b^2 = c^2, a i c uvek mogu, bilo koji da su brojevi, biti napisani kao a=x-y i c=x+y. u tom slucaju b ne moze biti nista drugo nego b=2sqrt{xy}.
e sad ne znam da li ovo vec postoji, tj dal se koristi.
izvinjavam se jos jednom na gresci iz prethodnog posta.
[ Nedeljko @ 01.04.2013. 10:44 ] @
Ako te zanimaju Pitagorine trojke, tj. trojke prirodnih brojeva 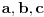 takve da je 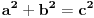 , opšti oblik za  deljivo manjim stepenom dvojke od  je
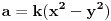 , 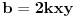 , 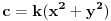
za neke prirodne brojeve 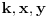 za koje je 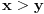 . [ number42 @ 01.04.2013. 15:15 ] @
aha, kontam, to je specijalan slucaj ove opste formule koju sam dao gore, a gde je x zamenjeno sa x^2 i y sa y^2, i a, b, i c pomnozeni koeficijentom 1/k.
pretpostavljam da je zanimljivo, ali, da li se (zasto se ne) upotrebljava opsti oblik?
(x-y)^2+(2sqrt{xy})^2=(x+y)^2
valjda, ako je sa dve promenljive, onda je prostije za razumevanje i resavanje nego sa tri kada je u obliku a^2 + b^2 = c^2.
[ darkosos @ 02.04.2013. 10:28 ] @
Primenio si formulu na sebe samu, sto obicno vodi do identiteta: 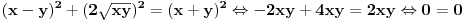 , za x i y vece od nule.
Mogao si isto tako da napises da je 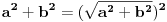 ... [ number42 @ 02.04.2013. 19:07 ] @
pa ne znam...
osnovna ideja mi je bila da dodjem do formule sa dve promenljive kojom ce se moci iz samo jedne stranice odrediti druge dve stranice pravouglog trougla. i to sam uspeo. eto recimo ova formula za pitagorine trojke koju je postavio nedeljko se direktno izvodi iz ove opste.
iz formule koju si ti postavio to nije moguce.
druga ideja mi je bila da to uopstim na bilo koji trougao. treca ideja je bila kako se kosinusna teorema moze obesmisliti, tj pojednostaviti. ovo bas ne znam da li fercera.
cetvrta ideja je bila da li se na ovaj nacin moze nekako resavati goldbahova hipoteza, i suprotna - da se svaki parni broj moze napisati kao razlika dva prosta. e s ovim zadnjim sam nadomak resenja :)
btw, kako radite to da vam izadju slicice formula, jel ima neka fora na forumu ili poseban program?
[ nightowl @ 02.04.2013. 22:54 ] @
[ darkosos @ 03.04.2013. 07:48 ] @
@number42
Posto je tvoja formula identitet, ne mozes je koristiti da izracunas ostale stranice na osnovu samo jedne... Ne znam da li si uopste pokusao? Evo recimo da je x=1, izracunaj ostale stranice trougla...
[ peromalosutra @ 03.04.2013. 08:08 ] @
Citat: osnovna ideja mi je bila da dodjem do formule sa dve promenljive kojom ce se moci iz samo jedne stranice odrediti druge dve stranice pravouglog trougla. i to sam uspeo.
Trebaju ti bar 3 informacije o trouglu da bi ga jedinstveno opisao, dakle stranica i 2 ugla, ili 2 stranice i ugao. [ whitie2004 @ 03.04.2013. 10:16 ] @
ma ne, :-)
to je specijalan slucaj zvani Euklid, a covek je pitao za opstu formulu i zakrivljen prostor ....
ako postoji, ne znam ni ja.
[ number42 @ 03.04.2013. 17:55 ] @
@nightowl, e hvala! ;)
@darkosos, naravno, slazem se. iz jednog dela stranice koji si dao  ne mozes saznati nista, ni druge stranice, pa ni tu samu stranicu.
[ darkosos @ 03.04.2013. 17:59 ] @
Napisao si da mozes iz jedne stranice da saznas ostale, to je zadatak... Ako ti smeta oznaka, stavi da je a=1 ili ako hoces, da je x-y=1, pa odredi ostale stranice...
[ number42 @ 03.04.2013. 18:04 ] @
@peromalosutra, da, tu su tri informacije - dve promenljive i prav ugao.
S tim sto si me sad bacio u razmisljanje - da li se za jednakokraki trougao mogu odrediti stranice iz ove formule (ako se posmatra kao dva identicna pravougla trougla sa zajednickom katetom).
e to bi onda bile dve informacije ako se ne varam? ili se "dva ugla su jednaka" racuna kao informacija pa su onda tri? ispravi me ako gresim slobodno.
@whitie2004, nisam pitao za zakrivljen prostor, krecemo se u okviru euklidske geometrije.
[ number42 @ 03.04.2013. 18:22 ] @
@darkosos, naravno da se iz jedne informacije ne moze nista zakljuciti, slazem se.
ali ovde imamo jednu stranicu (bilo koju iz opste formule 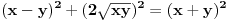 ) koju definisu dve informacije.
[Ovu poruku je menjao number42 dana 03.04.2013. u 22:18 GMT+1]
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|