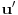
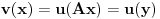
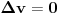
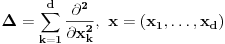
Da resimo i ovaj problem. Umesto koristicu, nekako prirodnu, oznaku . Dakle, zelimo da pokazemo da je funkcija harmonijska, odnosno gde je Laplasov operator. Neka je .

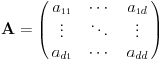
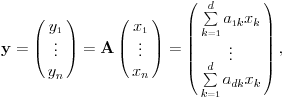
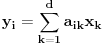
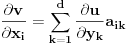
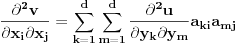
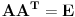
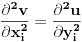
Tada je odnosno . Zato je (ovde smo koristili popularno chain rule pravilo za parcijalni izvod), odnosno . Odatle dobijamo (na ovom mestu koristimo da je matrica ortogonalna, tj. , zapisite taj uslov i videcete) , pa je, gle cuda, , tj. i je harmonijska funkcija.